Линейная и квадратичная интерполяция.
Локальная интерполяция состоит в том, что в рассмотрение принимается не все точки из таблицы, а лишь некоторые их подмножества, которые наиболее близко расположены от новой точки. Линейная интерполяция состоит в том, что заданные в таблице точки (xi;yi), (xi+1;yi+1) соед. Прямыми. Т.о. неизвестная функция заменяется ломанной линией с вершинами в узлах интерполяции. Уравнения каждого отрезка ломаной в каждом случае разные. Поскольку имеется n интервалов (xi-1,xi), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. Для любого i-го интервала, лежащего между (xi-1,yi-1) и (xi, yi) уравнение имеет вид:
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, которому принадлежит значение аргумента x, а затем подставить его в формулу y = aix + bi и найти приближенное значение функции в этой точке. Рассмотрим случай квадратичной интерполяции. В качестве интерполяционной функции на отрезке
Он содержит три неизвестных коэффициента ai,bi, ci. Для их определения необходимы три уравнения. Ими служат условия прохождения параболы через три точки: (xi-1, yi-1), (xi,yi), (xi+1, yi+1). Эти условия записываются в виде:
Решив эту систему уравнений, получим значения ai,bi,ci. Интерполяция для любой точки
|
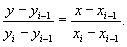
отсюда
принимается квадратный трехчлен. Этот вид интерполяции также называют параболической. Уравнение квадратного трехчлена:
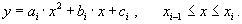
проводится по трем ближайшим к ней узлам.
