Метод состоит в следующем: по заданным табл. данным X0Y наносится система точек.
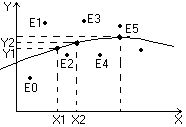 После этого проверяется линия, соответствующая внешнему виду j(x) и наиболее близко проходящая от заданных точек:
После этого проверяется линия, соответствующая внешнему виду j(x) и наиболее близко проходящая от заданных точек: 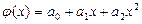
На проведённой линии выбираются новые точки, не принадлежащие системе табличных данных, а их число должно быть = кол-ву не известных параметров эмпирической функции. Значение координат в этих точках тщательно измеряются. Они используются для записи системы уравнений  , исходя из условия прохождения графика j(x) через эти точки. Решая полученную систему уравнений, находим неизвестные параметры
, исходя из условия прохождения графика j(x) через эти точки. Решая полученную систему уравнений, находим неизвестные параметры 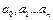 .
.
Другим методом является метод средних. Он базируется на предположении, что параметры 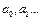 функции j(x) можно определить из равенства о суммы погрешности ei во всех точках Xi:
функции j(x) можно определить из равенства о суммы погрешности ei во всех точках Xi: 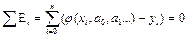 Из полученного ур. можно вычислить не известные параметры
Из полученного ур. можно вычислить не известные параметры 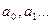 Однако, однозначно рассчитать все m+1 параметр из одного ур. нельзя. Поэтому полученные равенства путём группировки погрешностей eI разделяют на систему m-1 ур-я. Решая полученную систему, находим неизвестные параметры.
Однако, однозначно рассчитать все m+1 параметр из одного ур. нельзя. Поэтому полученные равенства путём группировки погрешностей eI разделяют на систему m-1 ур-я. Решая полученную систему, находим неизвестные параметры.

 После этого проверяется линия, соответствующая внешнему виду j(x) и наиболее близко проходящая от заданных точек:
После этого проверяется линия, соответствующая внешнему виду j(x) и наиболее близко проходящая от заданных точек: 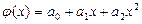
 , исходя из условия прохождения графика j(x) через эти точки. Решая полученную систему уравнений, находим неизвестные параметры
, исходя из условия прохождения графика j(x) через эти точки. Решая полученную систему уравнений, находим неизвестные параметры 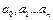 .
.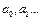 функции j(x) можно определить из равенства о суммы погрешности ei во всех точках Xi:
функции j(x) можно определить из равенства о суммы погрешности ei во всех точках Xi: 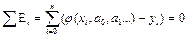 Из полученного ур. можно вычислить не известные параметры
Из полученного ур. можно вычислить не известные параметры 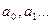 Однако, однозначно рассчитать все m+1 параметр из одного ур. нельзя. Поэтому полученные равенства путём группировки погрешностей eI разделяют на систему m-1 ур-я. Решая полученную систему, находим неизвестные параметры.
Однако, однозначно рассчитать все m+1 параметр из одного ур. нельзя. Поэтому полученные равенства путём группировки погрешностей eI разделяют на систему m-1 ур-я. Решая полученную систему, находим неизвестные параметры.


