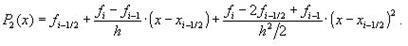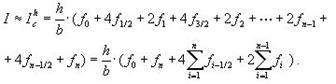Численное интегрирование.
Если функция f(x) непрерывна на отрезке [a;b] и ее можно выразить через известные функции, то для вычисления интеграла (1) можно воспользоваться формулой Ньютона- Лейбница:
Однако в действительности очень часто получить решение (1) с помощью формулы (2) или других аналитических методов невозможно. Примером может служить широко применяемый для исследования процессов теплообмена и диффузии, в статистической физике и теории вероятностей интеграл:
Помимо этого вычисления интеграла (1) в аналитической форме могут быть длительным и трудоемким процессом, приводящим к приближенному результату, или не дающими такового совсем. На практике помимо аналитических методов широко применяются специальные численные методы. Наиболее широко применяются квадратурные формулы вида:
Аi – числовые коэф., называемые весами квадратной формулы.
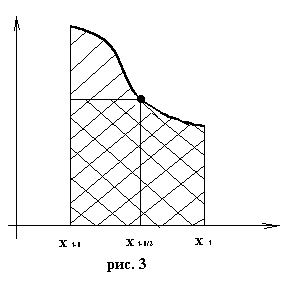
Разобьем отрезок [a;b] на элементарные отрезки [xi-1,xi ] точками При этом интеграл будет представлять сумму своих составляющих.
Будем считать шаг h=xi-x i-1 постоянным и введем обозначения fi = f (xi), fi-1/2 = f (xi-1/2), где xi-1/2 = (xi-1/2 + xi) / 2 - середина элементарного отрезка. Формула прямоугольников. Заменим приближенно площадь элементарной криволинейной трапеции площадью прямоуголника с основанием [xi-1, xi] и высотой fi-1/2.
Таким способом мы переходим к элементарной квадратурной формуле прямоугольников
В результате получаем замену площади исходной криволинейной трапеции площадью ступенчатой фигуры. Помимо формулы (4) на практике используют формулы левых и правых прямоугльников:
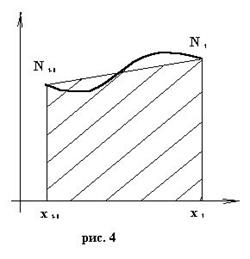
Формула трапеций. Соединим Ni-1 (xi-1, f i-1) и Ni(xi, fi) на графике функции y = f(x).
В результате получится трапеция (рис.4). Заменим приближенно площадь элементарной криволинейной трапеции площадью построенной фигуры. Получим элементарную квадратурную формулу трапеции:
Эта формула соответствует замене исходной фигуры (см. рис.1) ломанной линией, проходящей через точки N0,..., Nn. Формула Симпсона. Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки Ni-1, Ni-1/2,, Ni, то получим приближенное равенство:
Нетрудно убедиться, что верна формула:
Интегрирование этой формулы приводит к равенству:
которое представляет собой элементарную формулу Симпсона. От нее легко можно перейти к составной квадратурной формуле Симпсона:
|

 В прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла
В прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла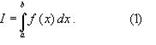 Он может выражать площадь, объем, работу переменной силы и т.д.
Он может выражать площадь, объем, работу переменной силы и т.д.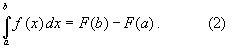
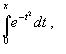 значение, которого не может быть выражено в виде конечной комбинации элементарных функций.
значение, которого не может быть выражено в виде конечной комбинации элементарных функций.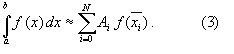
 - некоторые т., ∊[a; b] – узлы квадратной ф-лы;
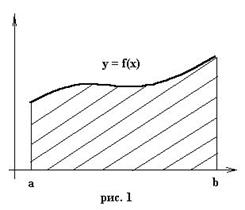
- некоторые т., ∊[a; b] – узлы квадратной ф-лы;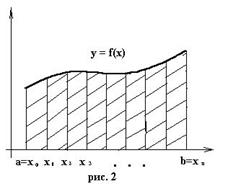 Выведем простейшие квадратурные формулы, исходя из геометрических соображений. Известно, что интеграл (1) - площадь криволинейной трапеции, ограниченная сверху функцией f(x) (рис.1).
Выведем простейшие квадратурные формулы, исходя из геометрических соображений. Известно, что интеграл (1) - площадь криволинейной трапеции, ограниченная сверху функцией f(x) (рис.1).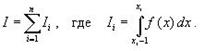
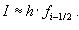 Произведя такую замену для всех элементарных криволинейных трапеций (рис. 2), получим составную квадратурную формулу прямоугольников:
Произведя такую замену для всех элементарных криволинейных трапеций (рис. 2), получим составную квадратурную формулу прямоугольников: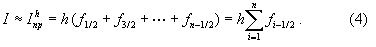
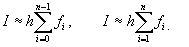
 Составная квадратурная формула трапеции будет представлять собой:
Составная квадратурная формула трапеции будет представлять собой:
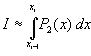 где P2 (x) - интерполяционный многочлен второй степени с узлами xi-1, xi-1/2, xi.
где P2 (x) - интерполяционный многочлен второй степени с узлами xi-1, xi-1/2, xi.