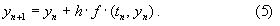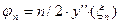Метод Эйлера.
Воспользуемся формулой Тейлора:
R(p+1)(t,h) - остаточный член. Если его отбросить, то получим приближенное равенство:
Если значение решения у в т. t известно, то в силу равенства (1) можно считать известными y’(t). Для нахождения производных
Использование приближенной формулы (3) приводит к формуле:
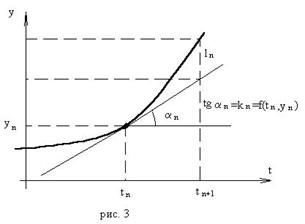
Метод Эйлера является первым и простейшим методом решения задачи Коши. Его можно получить, если в приближенном равенстве (4) положить p = 1, то есть оставить два первых слагаемых.Получим: Геометрическая интерпретация одного шага метода Эйлера заключается в аппроксимации решения на отрезке [tn, tn+1] касательной y=yn+y'(tn) (t-tn), проведенной в точке (tn,yn) к интегральной кривой, проходящей через эту точку. Таким образом, после выполнения N шагов неизвестная интегральная кривая заменяется ломаной линией, для которой угловой коэффициент kn очередного n - го звена равен значению f (tn, yn). (рис. 3) Погрешность аппроксимации в этом случае имеет вид:
|
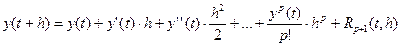(2)
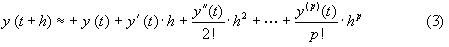
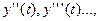продифференцируем Ур. (1) по t. Получим: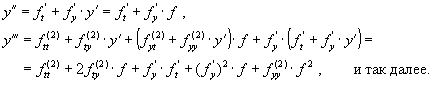
Выражения усложняются по мере роста порядка K.
