ДКЗ представляет собой задачу отыскивания реш. обыкновенного диф. ур. на отр. [а; б] при условии, что реш. заданы на обоих краях отрезка. Рассмотрим методы реш. задач этого класса, кот. можно записать в виде: U''(x)=f(x, u); на примере одномерного стационарного ур. теплопроводности:
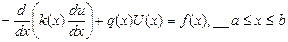 . Здесь k(x) играет роль коэф. теплопроводности,
. Здесь k(x) играет роль коэф. теплопроводности, 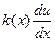 - плотность потока тепла. Помимо этого, указанное ур. может описать процесс диффузии газов, деформированию ступ и ступеней, распределение эл. магнитных волн, установившееся распределение плотности патронов в реакторе и многое другое.
- плотность потока тепла. Помимо этого, указанное ур. может описать процесс диффузии газов, деформированию ступ и ступеней, распределение эл. магнитных волн, установившееся распределение плотности патронов в реакторе и многое другое.
Предпримем, что ф-и q(x), k(x), f(x) известны и выполняется условие k(x)>0, q(x)>0. Тогда распределение температуры в стержне, описывание ф-ей f(x), м.б однозначно определено при задании состояния U(x) на границах отрезка [a, b], т.е U(a)=Ua, U(b)=Ub. Такие краевые условия наз. краевыми условиями 1-го рода. Часто краевую задачу записывают в операторном виде: 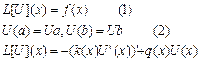 L[U](x) – диф. оператор
L[U](x) – диф. оператор

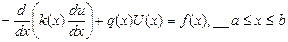 . Здесь k(x) играет роль коэф. теплопроводности,
. Здесь k(x) играет роль коэф. теплопроводности, 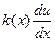 - плотность потока тепла. Помимо этого, указанное ур. может описать процесс диффузии газов, деформированию ступ и ступеней, распределение эл. магнитных волн, установившееся распределение плотности патронов в реакторе и многое другое.
- плотность потока тепла. Помимо этого, указанное ур. может описать процесс диффузии газов, деформированию ступ и ступеней, распределение эл. магнитных волн, установившееся распределение плотности патронов в реакторе и многое другое.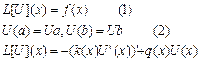 L[U](x) – диф. оператор
L[U](x) – диф. оператор


