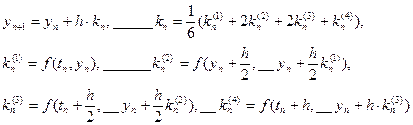Метод Рунге - Кутта.
Является наиболее популярным из одношаговых методов. Пусть y (t) - решение дифференциального уравнения y' = f (t,y), удовлетворяющее условию y (tn) = yn. Из формулы Ньютона - Лейбница
Если интеграл в формуле (6) можно было вычислить точно, то получилось бы простое выражение. Однако, в действительности это невозможно, поэтому будем строить приближенную формулу, заменив интеграл квадратурной суммой. Введем на отрезке [tn,tn+1] m вспомогательных узлов
Заменяя, входящий в равенство (6) интеграл квадратурной суммой с узлами tn(1),...,tn(m), получим приближенное равенство:
Однако воспользоваться равенством (7) нельзя, т.к. значения y в т.
Заменяя в этом равенстве для каждого i входящий в него интеграл соответствующей квадратурной формулой с узлами tn(1), tn (2),..., tn(i-1), получим приближенные равенства:
позволяющие последовательно вычислить приближения k y(tn(2)),..., y(tn(m)). Обозначим через yn(i) вспомогательные величины, являющиеся приближениями k y(tn(i)). Пусть kn(i) = f (tn(i), yn(i)) - приближение к значению углового коэффициента k в точке tn(i). В этом случае расчетные формулы примут вид:
Если выбросить вспомогательные величины yn(i), то те же формулы можно записать в виде:
Полученный метод носит название m - этапного метода Рунге - Кутта. Выбор конкретных значений параметров Метод Рунге - Кутта четвертого порядка точности:
|

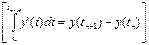 следует:
следует: 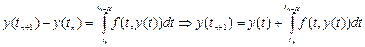 (6)
(6)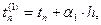
 где
где 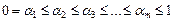
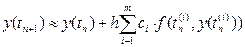 (7)
(7) неизвестны. Чтобы найти их запишем:
неизвестны. Чтобы найти их запишем: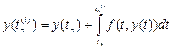
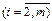 (8)
(8)
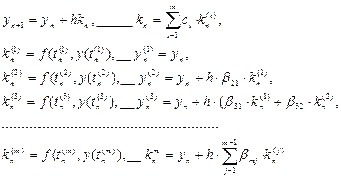
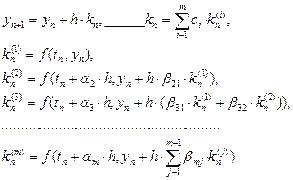
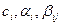 осущ. исходя из различных соображений, одним из кот. м. б. желание сделать порядок аппроксимации максимально возможным.
осущ. исходя из различных соображений, одним из кот. м. б. желание сделать порядок аппроксимации максимально возможным.