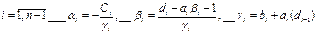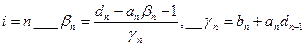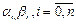Метод конечных разностей
Одним из широко распространенных методов реш. задачи (1) с ограничением (2) явл. метод конечных разностей. В этом методе область непрерывного аргумента заменяет конечным множеством точек (сеткой). После этого вместо ф-ии непрерывного арг. рассмотренные вводится ф-ия, определяющаяся только в узлах сетки (сеточная ф-ия). В этом случае произвед. м. б заменены своими разностными аналогами, т. е приближенно численными выражениями. В итоге исходная краевая задача заменяется дискретной краевой задачей или разностной схемой, представляющей собой сист. линейных и нелинейных алгебраич. ур., реш. кот. приблизительно принимает за реш. исходной задачи.
U(a)=Ua, U(b)=Ub (4) Заменим отрезок [a; b] непрерывного арг. Х сеткой, кот. обозначим
В результате реш. задачи 3 после подмены непрерывной ф-ии U(x) сеточной ф-ей будет найдена сеточная ф-я Uh, такая, что В результате диф. ур. (3) заменяется следующим: Будем считать, что ф-ия Uh во всех узлах сетки Wh удовлетворяет ур. (5). В этом случае ур. (5) явл. разностным ур. аппроксимации краевой задачи (1) с ограничением (2), фактически явл. системой линейной алгебры уравнений. Преобразуем ур. (5): -Ui-1 +Ui(2+h2qi)-Ui+1=h2fi.
Un=Ub Полученную систему удобно реш. методом прогонки. М-д прогонки предназначен для реш. трёх диагональных матриц: Прямой ход заключается в расчёте прогоночных коэф. α и β. На обратном ходе выч. знач. неизвестной ф-ии.
Значения ф-ии Ui выч. на обратном ходе: Un=βn Ui=αiUi+1+βi,
|
Зададим k(x)=1. В этом сл-е исх. задача примет вид. -U''(x)+q(x)U(x)=f(x) (3)
. 
где х0=а, хn=b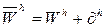
∂h – граница отрезка.
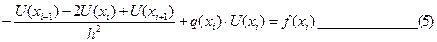
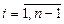
U0=Ua
