Во многих случаях мерой отклонения аппроксимирующей функции j(x) от некоторой функции f(x) вполне можно считать среднеквадратичное отклонение. Но бывают ситуации когда аппроксимирующий многочлен Pn(x) должен отклониться от непрерывной на отрезке [a,b] функции f(x) на расстоянии не больше заданной погрешности. В этом случае должно выполняться условие: 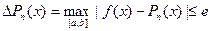 . В этом случае задача будет состоять в нахождении многочлена степени n для которого величина погрешности равномерного приближения минимальна. Такой многочлен называется многочлен наилучшего равномерного приближения.
. В этом случае задача будет состоять в нахождении многочлена степени n для которого величина погрешности равномерного приближения минимальна. Такой многочлен называется многочлен наилучшего равномерного приближения.
Теорема:
Для того чтобы некоторый многочлен Pn(x) был многочленом наилучшего равномерного приближения непрерывной на отрезке функции необходимо и достаточно чтобы на [a,b] нашлись как минимум n+2 точки такие что наша разность 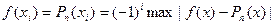 . Точки xi должны обладать следующими свойствами:
. Точки xi должны обладать следующими свойствами:
- В точках xi модуль погрешности приближения функции f(x) многочлена Pn(x) достиг. максимума.
- для всех точек при i=0,n п огрешность

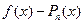 меняет знак при переходе от xi и xi+1.
меняет знак при переходе от xi и xi+1.

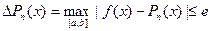 . В этом случае задача будет состоять в нахождении многочлена степени n для которого величина погрешности равномерного приближения минимальна. Такой многочлен называется многочлен наилучшего равномерного приближения.
. В этом случае задача будет состоять в нахождении многочлена степени n для которого величина погрешности равномерного приближения минимальна. Такой многочлен называется многочлен наилучшего равномерного приближения.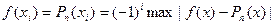 . Точки xi должны обладать следующими свойствами:
. Точки xi должны обладать следующими свойствами:
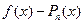 меняет знак при переходе от xi и xi+1.
меняет знак при переходе от xi и xi+1.


