 Использование многочленов высокой степени при решении задачи интерполяции связана с повышением сложности вычислений. Помимо этого необходимы спец методы составления подобных многочленов. Дополнительная трудность составляет накопление ошибок в округлении при проведении вычислений. Выходом может служить применение локальной интерполяции с использованием многочленов невысокой степени. Главным недостатком здесь явл. отличие производных в точках стыка двух соседних многочленов. В некоторых случаях эта особенность не играет большой роли при решении задачи интерполяции. Иногда быв. ситуации, требующие гладкости интерполяции многочлена. В этом случае в качестве интерполяции ф-и исп. сплайны, представленные собой спец образом построенные гладкие кусочно-многочленные ф-и, сочетающие в себе локальную простату и глобальную на всём отрезке [x0; xn] гладкость.
Использование многочленов высокой степени при решении задачи интерполяции связана с повышением сложности вычислений. Помимо этого необходимы спец методы составления подобных многочленов. Дополнительная трудность составляет накопление ошибок в округлении при проведении вычислений. Выходом может служить применение локальной интерполяции с использованием многочленов невысокой степени. Главным недостатком здесь явл. отличие производных в точках стыка двух соседних многочленов. В некоторых случаях эта особенность не играет большой роли при решении задачи интерполяции. Иногда быв. ситуации, требующие гладкости интерполяции многочлена. В этом случае в качестве интерполяции ф-и исп. сплайны, представленные собой спец образом построенные гладкие кусочно-многочленные ф-и, сочетающие в себе локальную простату и глобальную на всём отрезке [x0; xn] гладкость.
Пусть отрезок [x0; xn] разбит на n частей [xi-1; xi]. Тогда сплайном степени m Sm(x) наз. ф-ия, обладающая след. св-ми:
1. ф-ия Sm(x) непрерывна на всём отрезке от [x0; xm] вместе со своими производноми до некоторого порядка Р;
2. На каждом отрезке [xi-1; xi] сплайн совпадает с некоторым многочленом степени m. Sm(x)=Pm,i(x)
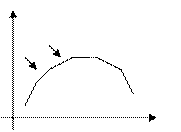
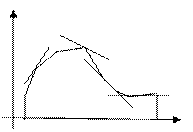
Разность теорем между степенью сплайна и наивысшей на отрезке (x0; xn) непрерывной производной наз. дефектом сплайна. Показанный на рисунке. Дефект сплайна = 1.
На практике наиб. распространенные кубич. сплайны с дефектом 1 или 2. На каждом отрезке такой сплайн совпад. с полиномом вида: 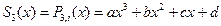
Значения 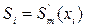 называется наклоном сплайна в точке xi. Т.о., отрезке (xi-1; xi) кубический сплайн однозначно определяется величинами
называется наклоном сплайна в точке xi. Т.о., отрезке (xi-1; xi) кубический сплайн однозначно определяется величинами 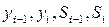
 (1)
(1)
Фактически задача сводится к определению наклонов сплайна Si-1 и Si: 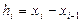
Если в т. xi, где 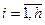 , нам известны не только величины
, нам известны не только величины 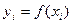 , но и величины
, но и величины 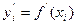 , то естественно предположить:
, то естественно предположить: 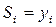 . Получаемый в этом случае сплайн называется локальным.
. Получаемый в этом случае сплайн называется локальным.
Можно потребовать, чтобы кубический сплайн имел непрерывную на отрезке от x0 до xn 2-ю производную. Для этого наклоны Si должны быть подобраны т.о., чтобы в т. стыка xi у соседних полиномов P3,i(x) и P3,i+1(x) совпадали значения 2-х производных: 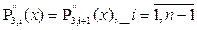 . Используя ф-лу (1), найдём выражения 2-х производных
. Используя ф-лу (1), найдём выражения 2-х производных 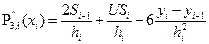
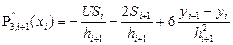
Приравниваем значения 2-х производных в т. стыка, получим систему из n-1 ур. для n+1 неизвестного:
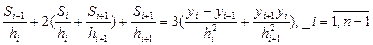
Полученная система явл. не доопределённой.
 Если известны численные значения
Если известны численные значения 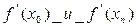 , то найденная система дополнилась бы 2-я ур.: для левой границы:
, то найденная система дополнилась бы 2-я ур.: для левой границы:
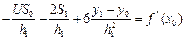
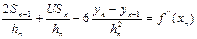
Если численные значения 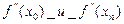 неизвестны, то полученную систему можно привести к системе, определяющий естественный кубический сплайн. В этом случае искусственно полагают вторые производные на границах отрезка x0 и xn = 0.
неизвестны, то полученную систему можно привести к системе, определяющий естественный кубический сплайн. В этом случае искусственно полагают вторые производные на границах отрезка x0 и xn = 0.

 Использование многочленов высокой степени при решении задачи интерполяции связана с повышением сложности вычислений. Помимо этого необходимы спец методы составления подобных многочленов. Дополнительная трудность составляет накопление ошибок в округлении при проведении вычислений. Выходом может служить применение локальной интерполяции с использованием многочленов невысокой степени. Главным недостатком здесь явл. отличие производных в точках стыка двух соседних многочленов. В некоторых случаях эта особенность не играет большой роли при решении задачи интерполяции. Иногда быв. ситуации, требующие гладкости интерполяции многочлена. В этом случае в качестве интерполяции ф-и исп. сплайны, представленные собой спец образом построенные гладкие кусочно-многочленные ф-и, сочетающие в себе локальную простату и глобальную на всём отрезке [x0; xn] гладкость.
Использование многочленов высокой степени при решении задачи интерполяции связана с повышением сложности вычислений. Помимо этого необходимы спец методы составления подобных многочленов. Дополнительная трудность составляет накопление ошибок в округлении при проведении вычислений. Выходом может служить применение локальной интерполяции с использованием многочленов невысокой степени. Главным недостатком здесь явл. отличие производных в точках стыка двух соседних многочленов. В некоторых случаях эта особенность не играет большой роли при решении задачи интерполяции. Иногда быв. ситуации, требующие гладкости интерполяции многочлена. В этом случае в качестве интерполяции ф-и исп. сплайны, представленные собой спец образом построенные гладкие кусочно-многочленные ф-и, сочетающие в себе локальную простату и глобальную на всём отрезке [x0; xn] гладкость.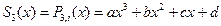
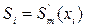 называется наклоном сплайна в точке xi. Т.о., отрезке (xi-1; xi) кубический сплайн однозначно определяется величинами
называется наклоном сплайна в точке xi. Т.о., отрезке (xi-1; xi) кубический сплайн однозначно определяется величинами 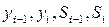
 (1)
(1)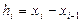
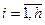 , нам известны не только величины
, нам известны не только величины 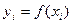 , но и величины
, но и величины 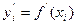 , то естественно предположить:
, то естественно предположить: 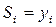 . Получаемый в этом случае сплайн называется локальным.
. Получаемый в этом случае сплайн называется локальным.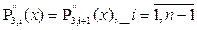 . Используя ф-лу (1), найдём выражения 2-х производных
. Используя ф-лу (1), найдём выражения 2-х производных 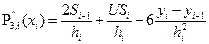
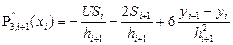
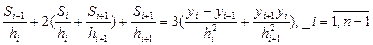
 Если известны численные значения
Если известны численные значения 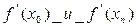 , то найденная система дополнилась бы 2-я ур.: для левой границы:
, то найденная система дополнилась бы 2-я ур.: для левой границы: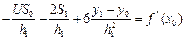
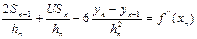
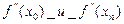 неизвестны, то полученную систему можно привести к системе, определяющий естественный кубический сплайн. В этом случае искусственно полагают вторые производные на границах отрезка x0 и xn = 0.
неизвестны, то полученную систему можно привести к системе, определяющий естественный кубический сплайн. В этом случае искусственно полагают вторые производные на границах отрезка x0 и xn = 0.


