Вопрос приближения функций. Понятие точечной и интерполяционной аппроксимации.
Если величина y является функцией аргумента x, то любому значению x из области определениясоответствует некоторое значение y. Однако, на практике часто неизвестна явная зависимость y от x, то есть ее невозможно записать в виде y = f(x). Бывают случаи, когда затруднительно использовать даже известную зависимость y = f(x). Наиболее распространенным случаем, когда вид связи между параметрами y и x неизвестен, является задание этой зависимости в виде таблицы { xi,yi }. В этом случае дискретному множеству значений аргумента соответствует множество значений функции {yi} полученные либо в результате расчетов, либо в экспериментов. Нам могут потребоваться значения функции y в точках отличных от xi., а это может быть затруднено. Таким образом, мы приходим к необходимости использования имеющихся табличных данных для приближенного вычисления значения y при любом значении параметра x, с помощью имеющейся табличных данных. Этой цели служит задача аппроксимации функции: функцию f(x) требуется приближенно заменить некоторой функцией φ(x) так, чтобы отклонение φ(x) от f(x) в заданной области было наименьшим. Функция φ(x) при этом называется аппроксимирующей. На практике часто эта функция представляется поленомом: В дальнейшем будем рассматривать только такую аппроксимацию. При этом коэффициенты ai будут подбираться так, чтобы достичь наименьшего отклонения графика от данной функции. Если приближение строится на заданном дискретном множестве точек {xi}, то аппроксимация называется точечной. При построении приближения на непрерывном множестве точек аппроксимация называется непрерывной (интегральной). Точечная аппроксимация. Одним из основных типов точечной аппроксимации является интерполяция. Она состоит в следующем: для заданной функции y=f(x) строится многочлен, принимающий в заданных точках xi те же значения yi, что и функция f(x), то есть При этом предполагается, что среди узлов нет одинаковых. Точки xi называются узлами интерполяции, а многочлен φ(x) - интерполяционным многочленом.
Как видно, при интерполировании основным условием является прохождение графика интерполяционного многочлена через данные значения функции в узлах интерполяции. Однако, в ряде случаев, выполнить данное условие затруднительно или нецелесообразно. Например, при большом количестве узлов интерполяции получается высокая степень многочлена. Кроме того, исходные данные могут содержать ошибку. Построение аппроксимирующего многочлена, с условием обязательного прохождения его графика через узлы интерполяции, означает повторение имеющейся ошибки. Выходом является исполнение апроксимирующей зависимости, график которой проходит "близко" от узлов интерполяции. Одним из видов такой зависимости является среднеквадратичное приближение функции с помощью мноочлена степень которокго меньше количества узлов апроксямации.
|

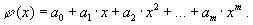
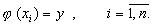
 Таким образом, близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек. Если максимальная степень интерполяционного поленома равна n-1; то говорят о глобальной интерполяции, так как один многочлен
Таким образом, близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек. Если максимальная степень интерполяционного поленома равна n-1; то говорят о глобальной интерполяции, так как один многочлен 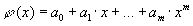 используется для замены функции f(x) на всем интервале изменения xi . Коэффициенты aj поленома можно найти из СЛАУ вида yi= φ(xi), при условии xi=xj, j≠i. Как правило, интерполяционные многочлены используются для аппроксимации функции в промежуточных точках между крайними узлами интерполяции, то есть при x0 < x < xn. Однако, иногда они используются для приближенного вычисления функции вне рассматриваемого отрезка
используется для замены функции f(x) на всем интервале изменения xi . Коэффициенты aj поленома можно найти из СЛАУ вида yi= φ(xi), при условии xi=xj, j≠i. Как правило, интерполяционные многочлены используются для аппроксимации функции в промежуточных точках между крайними узлами интерполяции, то есть при x0 < x < xn. Однако, иногда они используются для приближенного вычисления функции вне рассматриваемого отрезка  . Этот вид аппроксимации называют экстраполяцией.
. Этот вид аппроксимации называют экстраполяцией.


