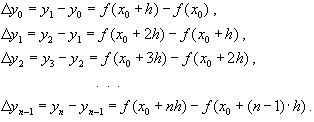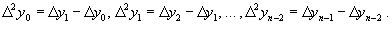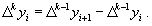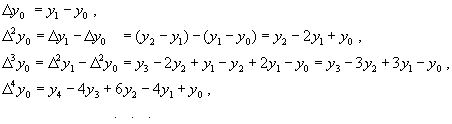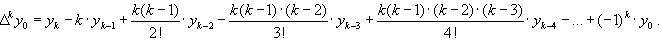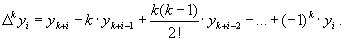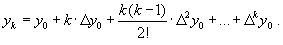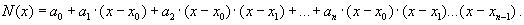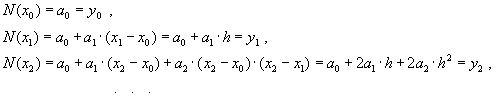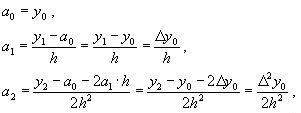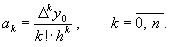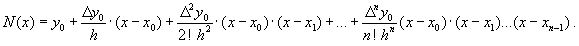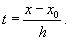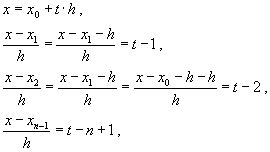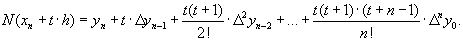Многочлен Ньютона с конечными разностями

В рассмотренных выше методах не делалось никаких предположений о плотности распределения узлов интерполяции. Рассмотрим случай равноотстоящих узлов интерполяции, то есть x_i - x_i-1 = const = h, i=1,n. h - называется шагом.

Введем понятие конечных разностей. Пусть некоторая функция задана таблицей. Составим разности значений функции:

Эти разности называются разностями первого порядка. Можно составить разности второго порядка:

Аналогично составляются разности k-го порядка:

Выразим конечные разности непосредственно через значение функции:

Таким образом, для любого k можно записать:

Запишем эту формулу для значений разности в узле x_i:

Используя конечные разности можно определить

Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде:

График многочлена должен проходить через заданные узлы, то есть N(x_i)=y_i(i = 0,n). Используем эти условия для нахождения коэффициентов многочлена:

Найдем отсюда коэффициенты a_i:

Таким образом для любого k-го коэффициента формула примет вид:

Подставляя эти формулы в выражение многочлена Ньютона получим его следующий вид:

Полученную формулу можно записать в упрощенном виде. Для этого введем переменную

В этом случае:

С учетом этих соотношений формулу многочлена Ньютона можно записать в виде:

Полученная формула называется первым интерполяционным многочленом Ньютона для интерполяции вперед.

Эту интерполяционную формулу обычно используют для вычисления значений функции в точках левой половины рассматриваемого отрезка. Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае t=(x-x_n)/h<0 и интерполяционный многочлен Ньютона можно получить в виде: