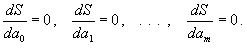Метод наименьших квадратов. Для определения параметров эмпирической ф-лы а0,а1, ,ам запишем сумму квадратов отклонений во всех точках xi
Для определения параметров эмпирической ф-лы а0,а1,…,ам запишем сумму квадратов отклонений во всех точках xi, i=0, n:
Параметры a0,a1,...,am будем искать при условии минимума функции S =S(a0,a1,...,am).
Поскольку в этом случае параметры a0,a1,...,am выступают в роли независимых переменных функции S (1), то ее min найдем, приравнивая к 0 частные производные по этим переменным:
Полученные соотношения представляют собой систему уравнений для определения a0,a1,...,am. На практике широко распространен случай, когда в качестве ЭФ используется полином:
Рассмотрим применение МНК для этого случая. Построим сумму квадратов для отклонений:
Найдем частные производные функции S=S(a0,a1,...,am).
Приравнивая к 0 эти выражения и собирая коэффициенты при неизвестных a0,a1,...,am, получаем систему уравнений:
Решая полученную СЛАУ получим коэффициенты a0,a1,...,an многочлена S=S(a0,a1,a1,...,an), которые являются исходными параметрами эмпирической формулы.
|