Общая постановка задачи Коши.
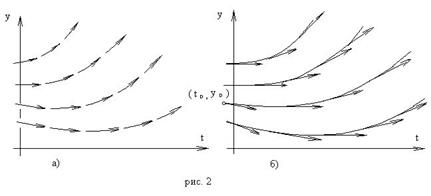
При рассмотрении технических систем и технологических процессов инженеру часто приходится сталкиваться с их характеристиками, которые непрерывным образом меняются во времени t. Такие явления подчиняются физическим законам, описываемым дифференциальными уравнениями. Одной из основных математических задач, решаемых для таких уравнений, является задача Коши. Обычно, к ней приходят, когда известно начальное состояние системы в момент времени t0 и требуется предсказать ее поведение в момент времени t > t0. Рассмотрим задачу Коши для дифференциального уравнения первого порядка: Решением уравнения (1) является дифференцируемая функция y(t), которая при подстановке в уравнение (1) превращается в тождество. График y(t) Заметим, что уравнение (1) задает в каждой точке (t, y) тангенс угла наклона касательной к графику решения, проходящего через эту точку. Если в каждой точке (t, y) задать с помощью некоторого вектора направление касательной, определенной значением f (t, y), то получится поле направлений.
Геометрическая задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Для того чтобы выделить из семейства решений дифференциального уравнения (1) конкретное решение, задают начальное условие: y(t0)=y0
|
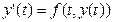(1)
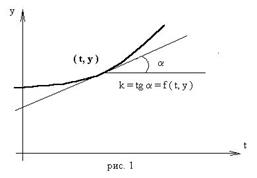называется интегральной кривой рис. (1), а процесс решения называется интегрированием.
