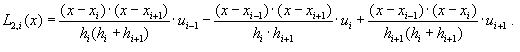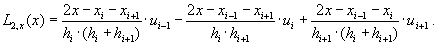Численное дифференцирование.Во многих задачах решение включает необходимость вычисления производных. Если функциональная зависимость f(x) имеет простой вид, то в вычислительных алгоритмах можно использовать явный вид производной f`(x) для определения ее числовых значений. Однако, в реальных ситуациях, функция f(x) может быть представлена математической моделью или конечным множеством точек (xi; fi(x)). В этом случае отсутствует возможность пользоваться аналитическим выражением производной. Вспомним определение производной: можно использовать приближенное числовое значение:
Вторую производную в точке xi можно рассчитать по этой же формуле:
Данные формулы дают достаточно высокую точность при задании h→0. отдельный случай представ. Случай когда функция f(x) задана таблицей. Здесь отсутствует возможность определения ∆x. Выходом в данной ситуации может быть использование интерполяционных методов. Покажем использование алгоритма Лагрнажа L2,i(x), проходящего по точкам xi-1,xi,xi+1.
Значение производной f'(x) будет приближенно совпадать с L2,i(x).
|
- производная слева
- справа
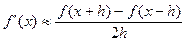
и так далее.
