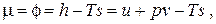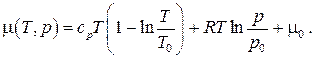Химический потенциал и его свойства
До сих пор нами рассматривались закрытые системы, в которых масса оставалась постоянной. Однако очень часто приходится иметь дело с системами, в которых число частиц и масса переменны (открытыми системами). Причинами изменения массы являются массообмен через оболочку системы, фазовые превращения, излучение, химические реакции, ядерные реакции. Пусть однокомпонентная однофазная термодинамическая система является открытой, однородной и равновесной. Изменение внутренней энергии такой системы будет происходить не только вследствие подвода теплоты и совершения над ней работы, но также и вследствие изменения ее массы в силу того, что вещество, проникающее через оболочку, обладает энергией, а фундаментальные уравнения Гиббса для термодинамических потенциалов следует дополнить еще одним слагаемым, пропорциональным изменению массы системы:
Величина μ, определяемая частными производными
носит название химического потенциала и имеет смысл изменения энергии термодинамической системы при изменении ее массы на единицу при поддержании постоянной той или иной пары независимых термодинамических параметров системы. Найдем связь химического потенциала с другими термодинамическими потенциалами системы. Запишем свободную энергию Гиббса Φ, энтропию S и объем системы V через их удельные величины:
Заменяя дифференциал свободной энергии Гиббса его выражением
Для удельных величин
т.е. химический потенциал вещества есть его удельная свободная энергия Гиббса. Для идеального газа, используя выражения для энтальпии и энтропии, химический потенциал будет иметь вид
Лекция 10
|

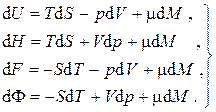
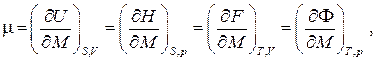

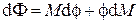 и перегруппировав слагаемые, получим
и перегруппировав слагаемые, получим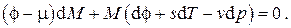
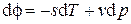 , откуда, ввиду произвольности дифференциала массы d M, находим
, откуда, ввиду произвольности дифференциала массы d M, находим