ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ КАНОНИЧЕСКИХ УРАВНЕНИЙ
Коэффициенты и свободные члены канонических уравнений метода перемещений rik и Rip по физическому смыслу, как уже отмечалось, могут быть двух видов - реактивные моменты в дополнительных заделках и реактивные силы в дополнительных линейных связях. Их определение, как и определение любых реакций, может быть выполнено на основе уравнений равновесия либо всей системы, либо какой-то её части (статический способ). Как показывает опыт, удобнее рассматривать равновесие отдельных частей основной системы метода перемещений, находящейся под тем воздействием, от которого определяется искомое реактивное усилие. При этом для реактивных усилий в дополнительных связях в методе перемещений применяется следующее правило знаков - реактивное усилие считается положительным, если его направление совпадает с направлением перемещения соответствующей дополнительной связи. При определении неизвестные реактивные усилия следует всегда направлять в положительных направлениях, используя их в дальнейшем с полученными знаками. В соответствии с изложенным, определение величин rik и Rip, пред-ставляющих по смыслу реактивные моменты в заделках, удобнее всего выполнять на основе рассмотрения равновесия узлов, в которых установлены соответствующие дополнительные заделки, предварительно вырезав эти узлы; в качестве уравнений равновесия при этом составляются суммы всех моментов, действующих на узлы, включая внешние сосредоточенные моменты и внутренние изгибающие моменты в сечениях, с помощью которых узлы вырезаются; из этих уравнений и определяются искомые реактивные моменты. Так, для рамы на рис. 10 при определении коэффициента r 11, представляющего собой реактивный момент в 1-ой дополнительной заделке от ее же поворота на единичный угол, необходимо вырезать узел 1 из эпюры
коэффициент r 12 найдем из вырезания узла 1 на эпюре
для определений свободного члена R 1 P необходимо вырезать 1-ый узел на эпюре МP (рис. 10к)
Таким образом, первый индекс искомого коэффициента или свободного члена здесь, по существу, показывает номер узла, который надо вырезать для определения этого коэффициента или свободного члена, а второй индекс указывает на эпюру, из которой этот узел надо вырезать. Казалось бы, что и коэффициенты (свободные члены) канонических уравнений, представляющие по смыслу реактивные силы в дополнительных линейных связях, также будет удобно определять из вырезания узлов, в которых эти связи установлены. Но оказывается это не совсем так. Например, для определения коэффициента r 22, являющегося реактивной силой во 2-ой дополнительной линейной связи от ее же единичного смещения, можно, конечно, вырезать узел 2 на эпюре М 2 (рис. 11); в результате чего получим:
Величину Q 23 легко определить по эпюре М 2, используя, например, формулу
Рис. 11 где: Q 0 учитывает действие распределенной нагрузки q на участке, т.е. это эпюра (закон изменения) поперечных сил на участке, как в простой двухопорной балке (если q нет, то Q 0 = 0); Мпр, Млев - ординаты изгибающих моментов справа и слева по концам участка; L - длина участка; знак перед абсолютной величиной принимается по следующему правилу: если стержень, на котором построена рассматриваемая эпюра М, для совмещения его с прямой, соединяющей ординаты Мпр и Млев по кратчайшему пути необходимо поворачивать по часовой стрелке, то принимается знак "+", если против часовой стрелки, то знак "-"; в результате получим:
Следует заметить, что величину Q 23 можно получить и через опорную реакцию в стержне 2-3 от действия заданного смещения Z 2 = 1, учитывая, что поперечная сила в приопорном сечении равна по величине реакции соответствующей опоры, которая представлена в табличных эпюрах; знак же поперечной силы при этом определяется по обычному правилу знаков для Q или по эпюре М. Для определения же величины продольной силы N 12 в стержне 1-2 необходимо вначале по эпюре М2, используя формулу (4), построить эпюру поперечных сил Q 2, после чего можно будет найти из вырезания узлов величину N 1–2; этот процесс, как видим, достаточно трудоемок. Проще будет процедура определения коэффициентов rik, Rip, представляющих собой реакции в линейных связях, если вырезать не узлы, а части основной системы метода перемещений таким образом, чтобы в уравнения равновесия этих частей, используемые для определения rik, Rip, входили только поперечные силы; при этом в качестве уравнений равновесия удобнее всего использовать сумму проекций сил на ось, параллельную искомой реактивной силе.
Заметим, что значения rik и Rip можно определить и с помощью формулы Мора [1]. При этом величины коэффициентов rik вычисляются по формулам
а величины свободных членов RiP по формуле
|

 , (построенной от поворота 1-ой заделки на единичный угол) (см. рис. 10з), из равновесия которого получим:
, (построенной от поворота 1-ой заделки на единичный угол) (см. рис. 10з), из равновесия которого получим: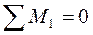 ;
; 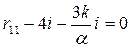 ;
; 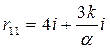 ;
;
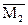 (рис. 10и):
(рис. 10и):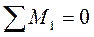 ;
; 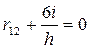 ;
; 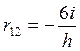 ;
;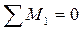 ;
; 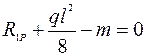 ;
; 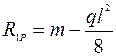 .
. ; r 22 - Q 23 - N 12 = 0; r 22 = Q 22 + N 12 .
; r 22 - Q 23 - N 12 = 0; r 22 = Q 22 + N 12 .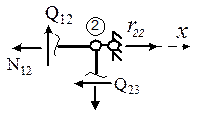
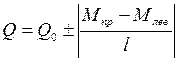 , (4)
, (4)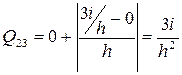 .
. Так, для определения коэффициента r 21 удобно вырезать из эпюры М 1 верхнюю часть, показанную на рис. 10л, из рассмотрения равновесия которой получим
Так, для определения коэффициента r 21 удобно вырезать из эпюры М 1 верхнюю часть, показанную на рис. 10л, из рассмотрения равновесия которой получим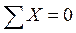 ;
; 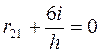 ;
; 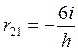 .
.
 Аналогично найдем также коэффициент r 22 (рис. 10м) и свободный член R 2 P (рис.10н), вырезав соответствующие части основной системы из эпюр М 2 и МP:
Аналогично найдем также коэффициент r 22 (рис. 10м) и свободный член R 2 P (рис.10н), вырезав соответствующие части основной системы из эпюр М 2 и МP: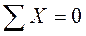 ;
; 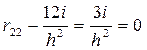 ;
; 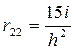 ;
;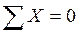 ;
; 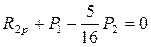 ;
; 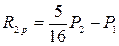 .
.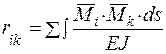 ;
; 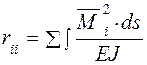 , (5)
, (5)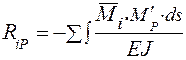 , (6)
, (6) где
где 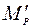 - эпюра изгибающих моментов от внешней нагрузки в статически определимой системе, полученной из заданной системы или основной системы метода перемещений удалением лишних связей и в том числе обязательно той связи, реакция которой определяется.
- эпюра изгибающих моментов от внешней нагрузки в статически определимой системе, полученной из заданной системы или основной системы метода перемещений удалением лишних связей и в том числе обязательно той связи, реакция которой определяется.


