ОСНОВНАЯ СИСТЕМА МЕТОДА ПЕРЕМЕЩЕНИЙОсновная система метода перемещений получается не отбрасыванием лишних связей, как это делается в методе сил, а наоборот, введением
что узел 1 с учетом установленных дополнительных связей и используемых допущений (раздел 1) будет вести себя так, будто в нем стоит полная действительная заделка, через которую никакие перемещения не передаются; аналогично узел 2 в О.С. имеет, по существу, шарнирно-неподвижную опору и через него никакие перемещения тоже передаваться не будут. Рис. 5 ! Таким образом, анализ показывает, что О.С. метода перемещений является статически неопределимой и, по существу, представляет собой совокупность отдельных независящих друг от друга однопролетных балочек с одним либо двумя защемленными концами вида:
Рис. 6 При этом изгибающие моменты в О.С. метода перемещений возникают только в тех балочках (только на тех участках), которые непосредственно подвержены какому-либо воздействию. На остальных же участках изгибающие моменты возникать не будут. Для рамы на рис. 3а основная система (О.С.) метода перемещений представлена рис. 3б.
|
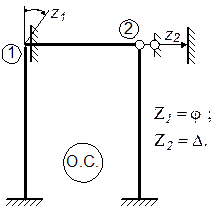Для рамы, представленной на рис. 1а, основная система (О.С.) метода перемещений имеет вид, изображенный на рис. 5. Анализ этой О.С. показывает,
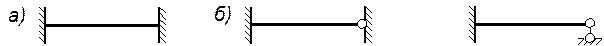или
