ВВЕДЕНИЕ. Метод перемещений при определении внутренних усилий в плоских статически неопределимых рамах: Методические указания по курсу «Строительная механика» для
Брест 2002
УДК 624.04 Метод перемещений при определении внутренних усилий в плоских статически неопределимых рамах: Методические указания по курсу «Строительная механика» для студентов строительных специальностей / Сост. В.И.Игнатюк; Брестский государственный технический университет. - Брест, 2002. - 32 с., 20 ил., 1 табл. В методических указаниях рассматривается расчет плоских статически неопределимых рам методом перемещений. Достаточно подробно изложены и анализируются все этапы расчета. Представлены достаточно полные таблицы балочных эпюр метода перемещений. Приведены примеры расчетов. Методические yказания предназначены для студентов строительных специальностей дневной и заочной форм обучения.
Составитель: В.И. Игнатюк, доцент, к.т.н.
Рецензенты: А.А. Борисевич, зав. кафедрой строительной механики Беларусского национального технического университета, д.т.н., доцент; Л.В. Кулаго, старший преподаватель кафедры строительной
© Брестский государственный технический университет 2002
ВВЕДЕНИЕ Метод перемещений имеет широкое распространение, особенно при расчете сложных статических неопределимых систем с большим количеством лишних связей, обладающих малой подвижностью узлов- сложных каркасных рам, ферм с жесткими узлами и т.д. Метод перемещений явился основой для разработки ряда ценных приближенных методов расчета рам - методов Кани, Кросса и др. Существует две формы решения задач по методу перемещений: каноническая и развернутая. Более удобной является каноническая форма метода перемещений, которая аналогична по форме записи уравнений методу сил. Свое развитие она получила в трудах Н.М. Рабиновича, А.А. Гвоздева, А.Ф. Смирнова. Ниже рассматривается именно эта форма метода перемещений. 1. ПОДХОДЫ И ДОПУЩЕНИЯ, При расчете статически неопределимых систем методом сил за неизвестные принимаются усилия в лишних связях, после определения которых легко находятся внутренние усилия (M, Q, N) в любом сечении системы, а также может быть найдено перемещение любой точки системы. Но задача может быть решена и в обратном направлении. Если сначала выявить деформированный вид системы, или определяющие этот вид перемещения системы, то затем можно установить соответствующее им распределение внутренних усилий, что иллюстрирует и широко известная зависимость M = EJ y";. Именно такой подход и используется в методе перемещений. При этом анализ показывает, что деформированный вид системы будет полностью определен, если будут известны угловые и линейные перемещения ее узлов. Это объясняется тем, что перемещения узлов равны перемещениям концов стержней, соединяющихся в этих узлах, а деформации стержней полностью и однозначно определяются перемещениями концов стержней. Последнее относится и к загруженным стержням, для которых, правда, деформированный вид будет зависеть дополнительно еще и от действующей нагрузки. Рассмотрим, например, раму, изображенную на рис.1. Деформированное состояние этой рамы определяется линейными и угловым перемещениями узлов 1 и 2; при этом число этих перемещений зависит от допущений, используемых в методе. Так, в общем случае число перемещений, определяющих деформации рамы, здесь равно пяти (рис. 1б); в случае же неучета поперечных и продольных деформаций и неучета изменения длин стержней при их изгибе (влиянием этих величин для изгибаемых рамно-стержневых систем ввиду их малости обычно пренебрегают - классическая постановка задачи) число этих неизвест-ных перемещений равно двум (рис. 1в)-
Рис. 1
И все эти неизвестные независимые перемещения узлов и принимаются за неизвестные в методе перемещений, откуда пошло и название этого метода - метод перемещений (деформаций).
а) пренебрегается поперечными и продольными деформациями элементов системы при ее деформировании; б) принимается, что проекция изогнутого (деформированного) стержня на его первона- чальное направление равна первоначальной длине стержня (рис. 2); в) считается, что величина углов в жест- ких узлах в процессе деформирования систе- Рис. 2 мы не изменяется; г) углы поворота узлов и сечений стержней при деформации систем в виду их малости принимаются равными тангенсам этих углов. Следует отметить, что для многих статически неопределимых систем степень кинематической неопределимости ниже, чем степень статической неопределимости, а также, что метод перемещений при равном числе неизвестных несколько проще в расчете, чем метод сил. 2. ОПРЕДЕЛЕНИЕ СТЕПЕНИ КИНЕМАТИЧЕСКОЙ Степень кинематической неопределимости системы, то есть число неизвестных независимых угловых и линейных смещений узлов, величины которых надо определить для представления о деформированной схеме системы и соответственно для определения внутренних усилий, определяется по формуле: n = ny + nл. (1) Здесь: ny - число неизвестных независимых угловых смещений узлов, определяемое по числу жестких узлов метода перемещений в системе; при этом под жесткими узлами метода перемещений (далее и будем называть просто жесткими узлами) здесь понимают такие, в которых соблюдается два условия: - в которых жестко соединяются под любым углом два и более стержня; - в которых происходит изменение внутренних усилий (изгибающих моментов), неопределяемое исходя из обычных уравнений равновесия (статики). Например, в раме, изображенной на рис. 3а, жесткими узлами, удовлетворяющими указанным условиям, будут узлы 1, 2, 3, (ny = 3); для узлов же А, В, С не выполняется второе условие, так как они относятся, по существу, к статически определимым частям системы, в которых все усилия можно определить с помощью обычных методов расчета статически определимых систем.
Рис. 3 nл - число независимых неизвестных линейных смещений узлов системы, которое можно определять двумя способами: 1. По числу возможных независимых линейных смещений жестких Например, в раме на рис. 3а необходимо проанализировать возможность и независимость линейных смещений жестких узлов 1, 2, 3 и шарнирных узлов 4, 5 при произвольном возможном упругом деформировании этой системы: – узел 1 по вертикали смещаться не может, так как он закреплен от вертикального смещения с помощью стержня 1-Д, который на основе допущений а и б (см. раздел 1) не позволяет разойтись (сойтись) точкам 1 и Д, и защемления Д; - по горизонтали узел 1 может смещаться, так как стержни 1-2 и 4-3 могут изгибаться (горизонтальное перемещение узла 1 показано стрелкой с - узел 2 по вертикали не может смещаться на основе тех же рассуждений, что и для узла 1; – по горизонтали же узел 2 он может смещаться, учитывая, что стержни 1-2, 2-Д, 4-3 и 5-Е могут изгибаться (горизонтальное смещение узла 2 обозначено стрелкой и соответственно цифрой 2); - узел 3 по горизонтали может смещаться (по аналогии с узлом 2), но это его смещение будет таким же, как и горизонтальное смещение узла 2 (так как стержень 2-3, соединяющий узлы 2 и 3, на основе допущений а и б (раздел 1) не позволяет измениться расстоянию между этими узлами); - по вертикали узел 3, учитывая возможность упругого деформирования стержней 1-4, 2-3 и 3-5, может смещаться (показано стрелкой с цифрой 3); - шарнирный узел 4 в данном случае может смещаться как по горизонтали (но одинаково с узлом 1, т.к. - стержень 1-4 на основе допущений а и б не дает возможности точкам 1 и 4 разойтись), так и по вертикали (но вместе с узлом 3 - вследствие наличия стержня 3-4); - шарнирный узел 5 по аналогии вертикально вообще смещаться не может, а по горизонтали может смещаться только на такую же величину, как, узлы 2 и 3. Таким образом, для рамы на рисунке 3 имеем три независимых линейных смещений узлов (n л =3), а всего в итоге получаем шесть неизвестных при расчете ее методом перемещений: n = nу + nл = 3 + 3 = 6. 2. В ряде учебников для определения nл предлагается формула nл = Wшарнирной схемы системы = 3 Д – 2 Ш - С 0, (2) согласно которой nл равно степени свободы шарнирной схемы рамы, получаемой путем введения (врезания) шарниров во все жесткие узлы, включая опорные (в жесткие заделки), анализируемой рамы. Например, для рамы на рис. 1а шарнирная схема имеет вид, представленный на рис. 1г, в соответствии которому получим nл = Wш.сх.р. = 3 Д - 2 Ш - С 0 = 3∙3 - 2∙2 - 4 = 1. Для рамы же на рис. 4а, шарнирная схема представлена на рис. 4б, будем иметь: nл = Wш.сх.р.= 3 ∙4 - 2∙ 3 - 6 = 0. Однако анализ возможного деформирования рамы по первому способу показывает, что узлы 1 и 2 могут горизонтально смещаться. Таким образом, примене-
мгновенная изменяемость. Поэтому при использовании формулы (2) всегда необхо- Рис. 4. димо шарнирные схемы систем проверять на мгновенную изменяемость и в случае ее наличия вносить корректировку в получаемые значения nл. Учитывая, что этот вариант определения nл достаточно сложен, им пользоваться не рекомендуется, а предлагается во всех случаях применять первый вариант вычисления nл, который и прост, и надежен.
|

 и
и  .
.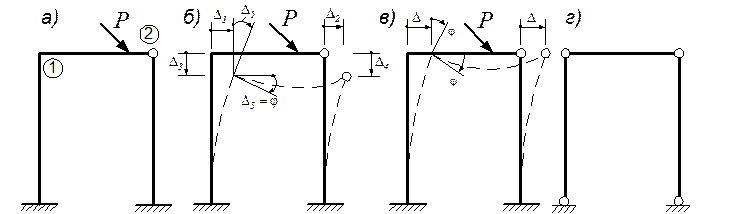
 ! Число независимых угловых и линейных смещений узлов, полностью и однозначно определяющих деформированный вид системы, называется
! Число независимых угловых и линейных смещений узлов, полностью и однозначно определяющих деформированный вид системы, называется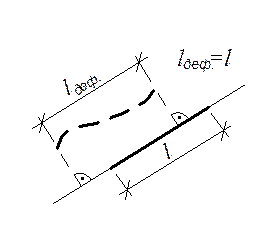 Отметим, что в классической форме метода перемещений, как впрочем и в методе сил, для рамностержневых систем, как уже указывалось, используются следующие допущения:
Отметим, что в классической форме метода перемещений, как впрочем и в методе сил, для рамностержневых систем, как уже указывалось, используются следующие допущения:
 ние формулы (2) приводит здесь к неверному результату, причиной которого является мгновенная изменяемость шарнирной схемы (рис. 4б) рамы. То есть формула (2) будет всегда давать неверные результаты в случаях, когда в шарнирной схеме рамы есть
ние формулы (2) приводит здесь к неверному результату, причиной которого является мгновенная изменяемость шарнирной схемы (рис. 4б) рамы. То есть формула (2) будет всегда давать неверные результаты в случаях, когда в шарнирной схеме рамы есть


