ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Бессонов Л. А. Теоретические основы электротехники.—М., 1978, том 1, § 8.31—&3&, 8.41—8,49 2. Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С. В. Основы теории цепей.—М., 1975, § 14.1—14.3. 3 Теоретические основы электротехники. /Под ред. Ионкина П. А.—М., 1976, том 1, § 16.1—16.3. 1. Изучить основные понятия операторного метода расчета: заданную функцию действительного переменного f(t) преобразуют специальным математическим приемом, в функцию комплексного переменного F(p). При этом f(t) называют оригиналом, F(р)- изображением. Вместо исходных дифференциальных уравнений получаются операторные уравнения для изображений; полученные операторные уравнения решаются относительно комплексного переменного F(р) для искомой функции; специальным математическим приемом осуществляется переход от функции комплексного переменного F(р) к ее оригиналу, т. е. к искомой функций времени f(t). Таким образом, сложные математические операции решения дифференциальных уравнений заменяются решением простых - алгебраических уравнений, записанных в операторной форме. Для преобразования функции вещественного переменного f(t) в функцию комплексного переменного F(р) пользуются преобразованием Лапласа.
Следует отметить, что между изображением и оригиналом нет равенства, а есть только соответствие. Это важное положение подчеркивается условной записью, связывающей изображение с оригиналом.
Имеются более 1500 оригиналов и соответствующих им изображений. Самые распространенные из них приведены в табл. 2. Заключительным этапом расчета переходных процессов операторным методом является нахождение оригинала функции по известному изображению. Это можно сделать по таблицам, приведенным в учебниках по ТОЭ, и в справочниках. При выполнении домашнего задания следует воспользоваться аналитическим методом перехода от изображения к оригиналу, а именно с помощью формулы разложения:
При выполнении домашнего задания следует воспользоваться аналитическим методом перехода от изображения к оригиналу, а именно с помощью формулы разложения:
Рассмотрите ряд примеров применения формулы разложения. Пример 5. Дано изображение
Найти оригинал f(t). Обозначим F1(р)=120; F2(р)=р2+160 р+6000. Найдем корни многочлена знаменателя F2(р)=0; р2 +160 р+6000=0;
Применим формулу разложения F1(p1)=F1(p2)=F1(p)=120. Производная знаменателя F2/ (р) == 2р +160. Подставляем в нее поочередно корни: F2/(p1)=2(-40)+160=40 F2/(p2)=2(-100)+160= - 40 По формуле разложения найдем оригинал:
Пример 6. Найти оригинал по заданному изображению:
Определяем корни знаменателя F2(р) = 0: р(р2+40р+500)=0; р1=о;
Вычисляем числитель, подставляя в него корни р1 р2, р3:
F1(р)=10р+200; F1(р1)=200; F1(р2)=10(-20+j10)+200=j100; Р1(Рз)= -j100, так как корни комплексные и сопряженные Вычисляем знаменатель:
Таким образом, подстановка в формулу разложения комплексных сопряженных корней приводит к получению в качестве оригинала затухающей синусоидальной функции. Итак, вычисление оригинала по формуле разложения следует вести в следующем порядке: 1) приравнивая F2(р) нулю, определяют корни p1, p2, p3и т. д.; 2) вычисляют производную знаменателя дроби F (р) и подставляют в нее поочередно корни p1, p2, p3...; 3) вычисляют числитель F1(р), подставляя в него корни p1, p2, p3...; 4) рассчитывают оригинал f(t), производя вычисления отдельных слагаемых и суммируя их. Изучив математические основы операторного метода интегрирования дифференциальных уравнений, рассмотреть его особенности для расчета переходных процессов в линейных цепях с сосредоточенными параметрами.
|

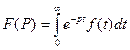

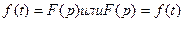
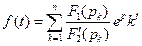 (29)
(29)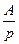


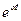

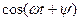

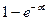
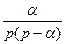
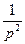

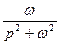



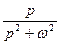




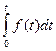
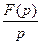
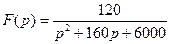



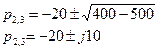
 Применяем формулу разложения:
Применяем формулу разложения:



