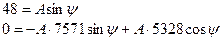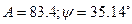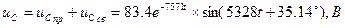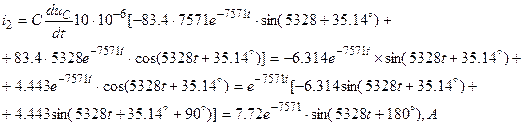Из уравнения (21) выразим
Уравнение (22) подставим в (21):
Сгруппировав члены и приведя их к общему знаменателю, получим дифференциальное уравнение второго порядка:
Характеристическое уравнение:
Проверка. Составим характеристическое уравнение по входному сопротивлению. Комплекс входного сопротивления запишем следующим образом:
Заменим jω на р. Тогда
а соответственно, Приравняв числитель к нулю, получим характеристическое уравнение (24). Подставив числовые данные, найдем корни характеристического уравнения:
Итак, корни комплексные и сопряженные:
5. Для нахождения искомого тока i2 предварительно найдем закон изменения напряжения на емкости:
Уравнение (25) дифференцируем:
Уравнения (25, 26) записываем при t=0+:
6. Для определения
Подставляем известные числовые значения:
Решив систему, уравнений, получим:
Так как
В систему уравнений-(27) подставляем числовые значения:
Решение дает:
Итак,
7. Определяем искомую величину i2
Примечание. При сложении двух синусоид удобно пользоваться символическим методом: записав их в комплексной форме, сложить полученные комплексные числа, а затем обратно перейти к синусоидальной функции.
|

 (22)
(22)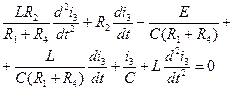
 (23)
(23)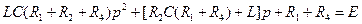 (24)
(24)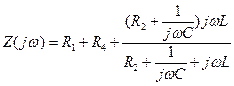
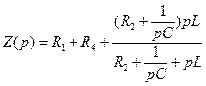
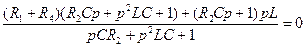
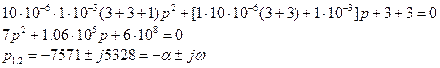

 (25)
(25)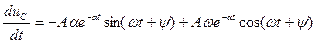 (26)
(26)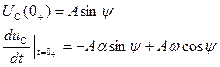 (27)
(27) систему уравнений (18......20) Кирхгофа записываем при t=0+:
систему уравнений (18......20) Кирхгофа записываем при t=0+:

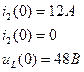
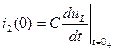 , то
, то