Освоить методику применения законов Ома и Кирхгофа в операторной форме.
Рассмотреть процесс включения последовательной цепи R, L, С на источник напряжения (рис. 17); при этом предположить, что конденсатор был предварительно заряжен и имел напряжение Uc(0). Для данной цепи по II закону Кирхгофа справедливо следующее уравнение:
Чтобы перейти к операторной форме, надо обе части уравнения (30) умножить на е-Рt и проинтегрировать от нуля до бесконечности. Интеграл справа разбить на сумму интегралов с учетом того, что
Уравнение (30) в операторной форме:
Откуда
Выражение (32) является законом Ома в операторной форме. называют операторным сопротивлением. Числитель этого выражения, помимо э. д. с., включенной в ветви, содержит еще два слагаемых: Li(0) и Запомнить, что эти слагаемые называют внутренними э. д. с. Они учитывают то, что в момент коммутации (при t=0) магнитное поле катушки и электрическое поле конденсатора обладали определенным запасом энергии. Таким образом, внутренние э. д. с. учитывают начальные условия. При нулевых начальных условиях закон Ома принимает вид
По первому закону Кирхгофа алгебраическая сумма мгновенных значений токов в ветвях, связанных в один узел, равна нулю:
Пусть изображение каждого из токов по Лапласу имеет следующий вид:
С учетом выражения (34), уравнение (33) в операторной форме принимает вид:
т. е. алгебраическая сумма изображений токов в ветвях, сходящихся в один узел, равна нулю. Уравнение (35) выражает первый закон Кирхгофа, записанный в операторной форме. По второму закону Кирхгофа в замкнутом контуре электрической цепи алгебраическая сумма падений напряжений равна алгебраической сумме э. д. с. Рассмотреть контур электрической цепи, содержащей n ветвей, каждая из которых содержит R, L, С и е. Составим для выбранного контура по второму закону Кирхгофа уравнение для мгновенных значений:
Полагая
где При нулевых начальных условиях второй закон Кирхгофа принимает следующий вид:
Следовательно, структура уравнения, составленного по второму закону Кирхгофа в операторной форме, такая же, как и в символической форме для комплексов действующих значений, только необходимо в операторной форме учитывать внутренние э. д. с.
|

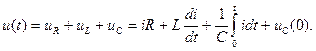 (30)
(30)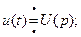
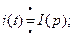
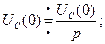
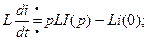
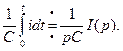
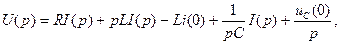 (31)
(31)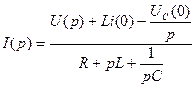 (32)
(32)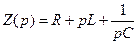 . Знаменатель выражения (32)
. Знаменатель выражения (32)
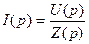
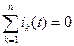 (33)
(33)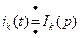 (34)
(34)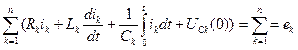 (36)
(36)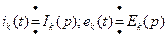 получить второй закон Кирхгофа в операторной форме:
получить второй закон Кирхгофа в операторной форме: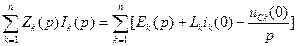 (37)
(37)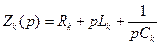 операторное сопротивление ветви.
операторное сопротивление ветви.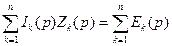 (38)
(38)


