Оценка истинного значения измеряемой величины по результатам эксперимента. Понятие случайной величины и вероятностного распределения
Предварительное ознакомление с классификацией погрешностей показывает, что измерение любой физической величины a необходимо проводить многократно. Допустим, что проведена серия n независимых, одинаково тщательных, прямых измерений, в результате которых получены значения x 1, x 2, x 3,... xn физической величины a. Тогда, как правило, наблюдается разброс данных около истинного значения, обусловленный существованием различных случайных факторов. Нанесем на числовую ось полученный ряд значений x 1, x 2, x 3,... xn в виде черточек (рис. 1а). На числовой оси этот ряд значений займет определенное место, и, очевидно, все значения как-то сгруппируются около искомого истинного значения измеряемой величины, положение которого отмечено вертикальной линией. Задача состоит в том, чтобы по данным x 1, x 2, x 3,... xn произвести оценку истинного значения измеряемой величины. Для решения этой задачи можно применить законы, установленные теорией вероятности по отношению к многократному повторению случайных явлений. В курсе теории вероятностей доказывается, что самой лучшей оценкой истинного значения является среднее арифметическое из числа измерений:
т.е. можно записать, что Эта запись означает, что истинное значение измеряемой величины а приближенно, но наилучшим образом оценивается по среднему арифметическому значению
Вероятнее всего, из расчета получится другое значение Это значение, вообще-то, не совпадает с двумя предыдущими средними значениями измеряемой величины. Таких серий равноточных независимых друг от друга измерений можно провести сколько угодно. Что же в конце концов послужит оценкой величины а? Ведь каждый раз мы будем получать среднее значение Таким образом, можно сделать очень важный вывод о том, что результат измерения является случайной величиной. Результат каждого отдельного измерения Результаты серии измерений одной величины можно наглядно представить, построив диаграмму, которая показала бы, как часто получались те или иные результаты. Такая диаграмма называется гистограммой. В качестве примера рассмотрим построение гистограммы по данным измерений величины ускорения силы тяжести методом математического маятника.
Таблица 1
Теперь представим себе, что число измерений неограниченно возросло и стало очень большим. Ширину интервалов можно сделать очень малой, но чтобы в каждом интервале было бы много отсчётов. Если теперь вместо гистограммы построить график, который давал бы относительную долю полного числа измерений В рассмотренном примере мы имели дело с последовательностью случайных событий, которые обнаруживают при неограниченном увеличении их числа характерную статистическую устойчивость. Обобщая сказанное, введем понятие случайной величины Х, как переменной величины, принимающей различные значения, зависящие от случайных факторов. На графике по оси абсцисс будем откладывать значения Х 1, Х 2, … Хn, полученные в результате n измерений физической величины, а по оси ординат – частоту появления Функция P (X) называется плотностью вероятности распределения. Смысл введенной функции P (X) состоит в том, что P (X). dX представляет относительную долю полного числа измерений n, приходящуюся на интервал (X, X + dX). Другими словами, P (X). dX есть вероятность того, что отдельное значение измеряемой величины находится в пределах интервала (X, X + dX). На рис. 3 изображена типичная кривая распределения результатов измерения физической величины, причем P (X). dX
площадью фигуры, заштрихованной наклонными линиями. Следовательно, вероятность того, что отдельное значение измеряемой величины окажется в интервале от X 1 до X 2, равна Как показывает опыт, в больших совокупностях равноправных объектов, которые называются статистическими ансамблями, существуют присущие им вероятностные распределения (распределение Максвелла для молекул идеального газа, распределение Ферми для электронов в металле, распределение Пуассона для распада радиоактивных атомов, распределение Бозе – Эйнштейна для теплового излучения, распределение Гаусса в случае большого числа измерений). Каждое из этих распределений математически описывается своей функцией плотности вероятности распределения P (X), имеющей конкретный математический вид в зависимости от характера случайной величины.
|

 , (1)
, (1)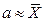 .
.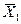 . Если повторить опыт, произведя вторую серию измерений, то, очевидно, получится новый ряд значений
. Если повторить опыт, произведя вторую серию измерений, то, очевидно, получится новый ряд значений 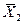 (рис. 1б), причем полученные значения сгруппируются около истинного, но не повторят картину первой серии измерений.
(рис. 1б), причем полученные значения сгруппируются около истинного, но не повторят картину первой серии измерений.
 :
: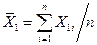 .
. , которое, также как и
, которое, также как и  , является наилучшей оценкой а, но в новой серии измерений. Наконец, из результатов третьей серии n измерений (рис. 1в) наилучшей приближенной оценкой истинного значения а будет
, является наилучшей оценкой а, но в новой серии измерений. Наконец, из результатов третьей серии n измерений (рис. 1в) наилучшей приближенной оценкой истинного значения а будет 
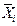 , лежащее где-то недалеко от а. Как видно из рис. 1, приближенные оценки
, лежащее где-то недалеко от а. Как видно из рис. 1, приближенные оценки 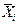 всегда более или менее отличаются друг от друга, т.е. испытывают случайное рассеивание, несмотря на кажущуюся неизменность условий в отдельных опытах.
всегда более или менее отличаются друг от друга, т.е. испытывают случайное рассеивание, несмотря на кажущуюся неизменность условий в отдельных опытах. невозможно заранее предсказать, однако, это еще не означает, что повторные измерения не обнаруживают никакой закономерности. Закономерность в распределении измерений существуети достаточно хорошо изучена. Она описывается законом нормального распределения
невозможно заранее предсказать, однако, это еще не означает, что повторные измерения не обнаруживают никакой закономерности. Закономерность в распределении измерений существуети достаточно хорошо изучена. Она описывается законом нормального распределения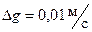 .
.
 , то получится гладкая кривая, называемая кривой распределения.
, то получится гладкая кривая, называемая кривой распределения.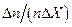 полученных значений в заданном интервале
полученных значений в заданном интервале 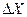 , приходящуюся на единицу этого интервала. Тогда в пределе при
, приходящуюся на единицу этого интервала. Тогда в пределе при  и
и  получим плавную кривую распределения для функции
получим плавную кривую распределения для функции 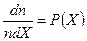 .
.
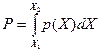 и представлена на рис. 3 площадью фигуры, заштрихованной горизонтальными линиями.
и представлена на рис. 3 площадью фигуры, заштрихованной горизонтальными линиями.


