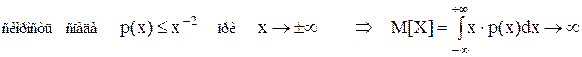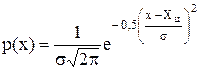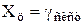Понятие центра распределения случайной погрешности
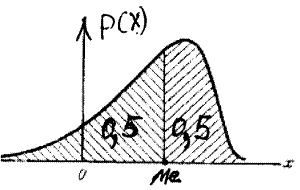
Характеристика в виде координаты центра распределения Xц определяет положение случайной величины на числовой оси, т.е. указывает некоторое среднее или типичное значение, около которого группируются все возможные значения случайной величины. Эта координата может быть определена несколькими способами. Медиана распределения. Наиболее общим является определение центра из принципа симметрии. Точка на оси x, слева и справа от которой вероятности появления различных значений случайной величины равны между собой и составляют 0,5, называется медианой. На графике интегрального закона распределения F(x) координата медианы соответствует пересечению кривой уровня 0,5. На графике дифференциального закона распределения p(x) координата медианы соответствует вертикали, делящей площадь ограниченную кривой распределения пополам.
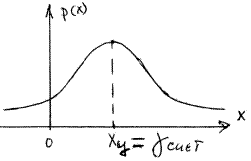
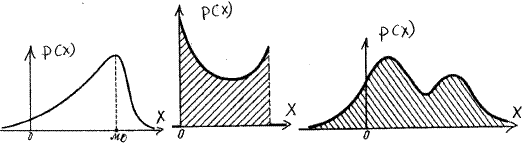
Мода распределения. Оценкой центра распределения Xц может служить значение случайной величины называемое модой, в котором плотность вероятности максимальна.
Такая оценка эффективна при симметричной или близкой к симметричной кривой плотности распределения, имеющей один максимум. Такое распределение называется модальным, если имеется более одного максимума, распределение называется полимодальным. Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом. Такие распределения называются антимодальными. Есть распределения, у которых не существует моды, например, равномерное распределение. В этих случаях определение центра как моды распределения лишено смысла.
Центр тяжести распределения. Координата центра Xц может быть определена как центр тяжести распределения – абсцисса или среднего арифметического:
Для определения математического ожидания случайной величины необходимо знать вероятности появления значений величины, что не всегда возможно на практике. Поэтому практически вместо МО часто используют более простое, но приближенное значение среднего арифметического полученных значений случайной величины. При увеличении числа опытов среднее арифметическое полученных значений случайной величины Х приближается (сходится по вероятности) к ее математическому ожиданию.
Сформулированная связь между средним арифметическим и математическим ожиданием составляет содержание одной из форм закона больших чисел. Однако, оценка центра распределения математическим ожиданием возможна не для всех распределений. Распределения, у которых
математического ожидания не существует, так как определяющий его интеграл расходится, например, распределение Коши. Понятие же центра распределения правомерно для всех распределений. В общем случае медиана, мода и математическое ожидание случайной величины не совпадают. В частном случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой Рассмотрим специфику применения понятия центра распределения применительно к погрешностям измерения. Ранее были приведены распределения с координатой центра Xц = 0. При Xц ¹ 0 изменяется аналитическое описание плотности распределения вероятностей. Так, плотность распределения Гаусса
Вероятностный метод описания используют в первую очередь для анализа случайных погрешностей. Однако достоинство такого подхода заключается в том, что метод подходит и для описания систематических погрешностей, является в этом плане универсальным и не требует предварительного разделения погрешностей на случайные и систематические составляющие. При вероятностном описании погрешности координата центра распределения Xц определяет значение систематической составляющей погрешности. Вероятностное описание погрешностей удобно тем, что включает в себя и указание ее систематической составляющей.
Если из распределения вычесть систематическую составляющую погрешности, т.е. перенести начало координат в центр распределения, то такое распределение называется центрированным.
|

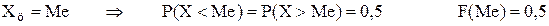


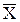 , относительно которой опрокидывающий момент равен нулю. Центр распределения случайной непрерывной величины, найденный таким путем, носит название математического ожидания (МО). Если провести механическую аналогию, то математическое ожидание M[X] - это координата центра тяжести данной системы материальных точек, опрокидывающий момент относительно которой равен нулю. МО определяют как первый начальный момент, вычисляя в случае непрерывной величины интеграл. МО или первый начальный момент представляет собой основную характеристику положения случайной величины. В случае дискретных отсчетов xi вычисление интеграла, заменяют вычислением соответствующей суммы, так называемым средним взвешенным из значений xi, причем каждое значение xi при осреднении должно учитываться с весом, пропорциональным вероятности pi этого значения.
, относительно которой опрокидывающий момент равен нулю. Центр распределения случайной непрерывной величины, найденный таким путем, носит название математического ожидания (МО). Если провести механическую аналогию, то математическое ожидание M[X] - это координата центра тяжести данной системы материальных точек, опрокидывающий момент относительно которой равен нулю. МО определяют как первый начальный момент, вычисляя в случае непрерывной величины интеграл. МО или первый начальный момент представляет собой основную характеристику положения случайной величины. В случае дискретных отсчетов xi вычисление интеграла, заменяют вычислением соответствующей суммы, так называемым средним взвешенным из значений xi, причем каждое значение xi при осреднении должно учитываться с весом, пропорциональным вероятности pi этого значения.