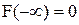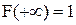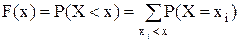Закон распределения и функция распределения

Рассмотрим случайную дискретную величину Х с возможными значениями x₁, x₂, x₃, …, x_n. Величина Х может принять каждое из них с некоторой вероятностью p_i, причем в результате опыта величина Х примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий:

Так как несовместные события образуют полную группу, то

т.е. сумма вероятностей всех возможных значений случайной величины равна единице. Эта суммарная вероятность распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если указать, какой вероятностью обладает каждое из событий. Этим мы установим так называемый закон распределения случайной величины.

Закон распределения случайной величины устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.

Для случайной дискретной величины удобно использовать закон распределения в виде ряда распределения. Однако эта характеристика не является универсальной т.к. она не существует для случайной непрерывной величины.

Для количественной характеристики распределения вероятностей непрерывной величины удобно воспользоваться не вероятностью события Х = x, а вероятностью события Х < x, где x — некоторая текущая переменная. Вероятность этого события, зависящая от x, называется функцией распределения случайной величины Х и обозначается:

Функцию распределения F(x) называют также интегральной функцией распределения или интегральным законом распределения.

Функция распределения — самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.

Некоторые о сновные свойства функции распределения.

Функция распределения F(x) есть неубывающая функция своего аргумента: !!

На минус бесконечности функция распределения равна нулю:

На плюс бесконечности функция распределения равна единице:

Рассмотрим случайную величину Х как случайную точку Х на оси 0х, которая в результате опыта может занять то или иное положение. Тогда функция распределения F(x) есть вероятность того, что случайная точка Х в результате опыта попадет левее точки x.

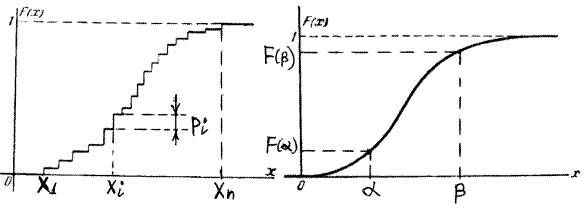
Будем увеличивать x, т.е. перемещать точку x вправо по оси абсцисс. Очевидно, при этом вероятность того, что случайная точка Х попадет левее x, не может уменьшиться; следовательно, функция распределения F(x) с возрастанием x убывать не может. Будем неограниченно перемещать точку x влево по оси абсцисс. При этом попадание случайной точки Х левее x в пределе становится невозможным событием; естественно полагать, что вероятность этого события стремится к нулю, т.е. . Аналогичным образом, неограниченно перемещая точку x вправо, убеждаемся, что , так как событие Х < x становится в пределе достоверным.

График функции распределения F(x) в общем случае представляет собой график неубывающей функции, значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки.

Зная ряд распределения дискретной случайной величины, можно легко построить функцию распределения этой величины

Неравенство x_i < x под знаком суммы указывает, что суммирование распространяется на все те значения x_i, которые меньше x.

Когда текущая переменная x проходит через какое-нибудь из возможных значений дискретной величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.

Функция распределения любой дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. Сумма всех скачков функции F(x) равна единице.

По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки — меньше; ступенчатая кривая становится более гладкой. В пределе при n ® ¥; случайная величина стремится к непрерывной величине, а ее функция распределения — к непрерывной функции.
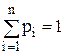
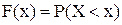
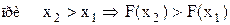