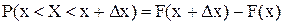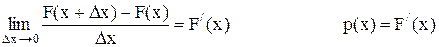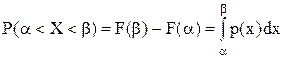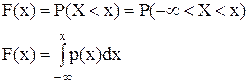Плотность распределения

Имеется непрерывная случайная величина Х с функцией распределения F(x), непрерывной и дифференцируемой. Вероятность попадания этой случайной величины на участок от x до x + Dx, равна приращению функции распределения на этом участке:

Отношение этой вероятности к длине участка, равно средней вероятности, приходящейся на единицу длины на этом участке. Если приближать к нулю длину участка, то в пределе получим производную от функции распределения:

Производная функции распределения, обозначаемая как функция p(x) характеризует плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения или плотностью вероятности непрерывной случайной величины Х. Функцию p(x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины Х.

Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.

Плотность распределения, так же как и функции распределения, есть одна из форм закона распределения.

В отличии от функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.

Учитывая соотношение

выразим вероятность попадания величины Х на отрезок от a до b через плотность распределения, используя формулу определенного интеграла:

Геометрически вероятность попадания величины Х на участок (a, b) равна площади кривой распределения, опирающейся на этот участок.

Ранее получена формула выражающая плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. Используя определение F(x) получим:

Геометрически F(x) есть площадь под кривой распределения, лежащая левее точки x.

Укажем основные свойства плотности распределения.

1.Плотность распределения есть неотрицательная функция:

Это свойство непосредственно вытекает из того, что функция распределения F(x) есть неубывающая функция.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

Геометрически это свойство плотности распределения означают, что полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Размерности функции распределения F(x) и плотности распределения p(x) случайной величины различны. Функция распределения F(x), как всякая вероятность, есть величина безразмерная. Размерность плотности распределения p(x) – величина, обратная размерности случайной величины.