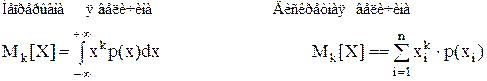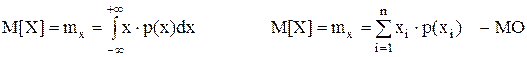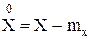Моменты распределения
Для описания различных свойств распределений используют характеристики законов распределения, называемые моментами. Моменты описывают определённое свойство распределения. Моменты, найденные без исключения систематической составляющей, называются начальными, а найденные для центрированных распределений, - центральными. Начальные моменты k –го порядка для случайной непрерывной величины выражаются интегралами, а для случайной дискретной величины суммами
Первый начальный момент называется математическим ожиданием M[X]. Для дискретных случайных величин: математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений. Для МО часто используют обозначение mx.
Начальные моменты порядка выше первого не нашли практического применения. Центрированной случайной величиной, называют отклонение случайной величины Х от ее математического ожидания mx:
Центрирование случайной величины, равносильно переносу начала координат в точку, координата которой равна математическому ожиданию. Центральные моменты k –го порядка для случайной непрерывной величины выражаются интегралами, а для случайной дискретной величины суммами
Первый центральный момент (математическое ожидание центрированной случайной величины) всегда равен нулю.
|