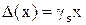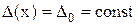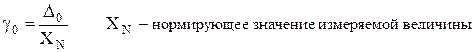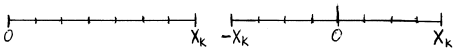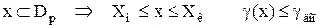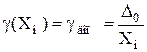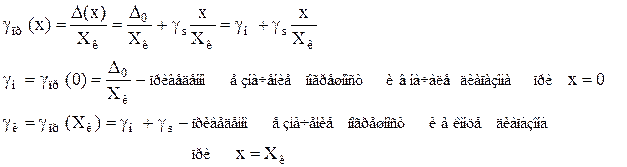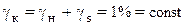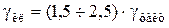Методы нормирования погрешностей средств измерений.

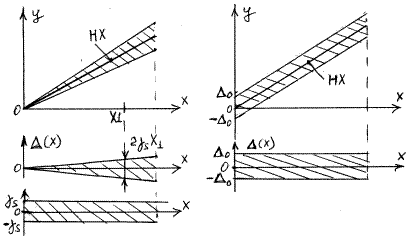
Нормированными значениями называют погрешности предельные для данного типа СИ. Погрешности отдельных экземпляров данного типа СИ могут различаться, однако в целом jyb не превосходят предельного значения. Таким образом нормируется основная и дополнительная погрешности. Именно эти значения основной погрешности, а также коэффициентов влияния и заносятся в паспорт каждого экземпляра СИ.

Класс точности средств измерений. Это характеристика, определяющая гарантированные границы значений основных и дополнительных погрешностей.

Основная погрешность СИ нормируется четырьмя различными способами в зависимости от соотношения аддитивной и мультипликативной составляющих в погрешности СИ.

При чисто мультипликативной полосе погрешностей СИ абсолютная погрешность D(x) возрастает прямо пропорционально текущему значению x измеряемой величины. Поэтому такой преобразователь имеет только мультипликативную погрешность, т.е. погрешность чувствительности. В этом случае относительная погрешность оказывается постоянной величиной при любом значении x и ее удобно использовать для нормирования погрешностей СИ и указания его класса точности.

Таким способом нормируются погрешности масштабных преобразователей – усилителей переменного тока, делителей напряжения, шунтов, измерительных трансформаторов тока и напряжения. Их класс точности указывается в виде значения g_s, выраженного в процентах. Граница относительной погрешности результата измерения g(x) в этом случае постоянна и при любом x равна значению g_s, а абсолютная погрешность результата измерения рассчитывается по формуле

При чисто аддитивной полосе погрешностей для любых значений x остается неизменной граница абсолютной погрешности нуля

Но нормировать абсолютное значение D₀ обычно неудобно, особенно для многопредельных приборов, где оно будет различным для каждого диапазона измерения. Поэтому нормируют не абсолютное D₀, а приведенное значение этой погрешности:

Если нулевая отметка находится на краю шкалы, то берут нормирующее значение X_N равным верхнему пределу диапазона измерений X_k. Если же нулевая отметка находится посредине шкалы, то X_N равно протяженности диапазона измерений 2X_k.

Значение приведенной погрешности g₀, выраженное в процентах, используется для обозначения класса точности таких СИ. Однако полагать, что вольтметр класса точности 1,0 обеспечивает во всем диапазоне измерений получение результатов с погрешностью ±1%, является грубой ошибкой т.к. эта погрешность является характеристикой самого вольтметра, а не полученного с его помощью результата измерения. Погрешность собственно результата измерения правильнее оценивать значением относительной погрешности.

В действительности текущее значение относительной погрешности растет обратно пропорционально измеряемой величине и изменяется по гиперболе.

Таким образом, относительная погрешность g(x) равна классу точности прибора g₀ лишь на последней отметке шкалы при x = X_к. При x = 0,1X_к она равна 10 g₀, а при дальнейшем уменьшении x стремится к бесконечности.

При уменьшении измеряемой величины x до значения абсолютной погрешности нуля D₀ относительная погрешность результата измерения достигает 100%. Такое значение измеряемой величины x = D₀ называется порогом чувствительности СИ. Порог чувствительности представляет собой изменение измеряемой величины, способное вызвать наименьшее обнаруживаемое изменение выходной величины. Считают, что значения входной величины меньше аддитивной погрешности неразличимы.

Полный диапазон измеряемой величины D_п для любого преобразователя ограничивается снизу порогом чувствительности, а сверху – пределом измерений. Так как в области малых значений x относительная погрешность измерений очень велика, то на практике используют рабочий диапазон измеряемой величины D_р. Рабочий диапазон ограничен снизу начальным значением X_н, при котором относительная погрешность измерений g(x) еще не превосходит некоторого заданного допустимого значения g_доп.

Допустимая относительная погрешность g_доп и начальное значение входной величины X_н связаны формулой

Полный диапазон D_п и рабочий диапазон D_р измеряемых величин можно записать в виде

В начальной части шкалы измерения недопустимы, в чем и заключается отрицательное влияние аддитивной погрешности, не позволяющее использовать один и тот же преобразователь для измерения как больших, так и малых измеряемых величин.

В случае чисто мультипликативной погрешности такого ограничения не существует: полный и рабочий диапазоны начинаются с x = 0.

При одновременном присутствии аддитивной и мультипликативной составляющих полоса погрешностей имеет трапецеидальную форму, а текущее значение абсолютной погрешности D(x) в функции измеряемой величины описывается соотношением:

Приведенное значение погрешности получим, разделив все члены уравнения на предел измерений X_к

Таким образом, при наличии у СИ и аддитивной и мультипликативной составляющих погрешности его приведенная погрешность линейно возрастает от g_н в начале диапазона до значения g_к = g_н + g_s в конце диапазона. Эта погрешность является характеристикой самого СИ, но не результата измерения как и в случае чисто аддитивной погрешности.

Точность результата измерения удобно характеризовать относительной погрешностью. Относительная погрешность будет иметь минимальное значение, равное значению приведенной погрешности g_к только в конечной точке диапазона x = X_к. По мере уменьшения x относительная погрешность будет возрастать до бесконечности.

Но, в отличие от чисто аддитивной погрешности, заметное возрастание g(x) начинается тем позже, чем меньше в суммарной погрешности доля аддитивной погрешности, т.е. чем меньше отношение

Изображены кривые возрастания g(x) при уменьшении x при разных значениях a для случая

Кривые показывают, как расширяется рабочий диапазон СИ D_р по мере уменьшения a, т.е. уменьшения доли аддитивной погрешности D₀ и приближения полосы погрешностей к чисто мультипликативной полосе. Трапециидальная полоса погрешностей характерна для высокоточных цифровых приборов, например, мультиметров, вольтметров.

При нормировании погрешностей сложных СИ двучленной формулой ГОСТ 8.401-80 предусматривает ее написание отличное от рассмотренного, более удобное для практического вычисления g(x). Текущее значение относительной погрешности g(x) выражается через приведенные погрешности в начале g_н и в конце g_к диапазона измерений.

В технической документации на СИ обычно приводят несколько иную форму записи формулы погрешности:

Специальные формулы нормирования погрешностей применяют для СИ, погрешности которых не могут быть нормированы предыдущими 3 способами.

Обозначения классов точности средств измерений. Согласно ГОСТ 8.401-80 для указания нормированных значений погрешности не могут использоваться произвольные числа. Выраженные в процентах, они могут иметь значения

(6 - 5 – 4 – 2,5 – 2 – 1,5 – 1)×10ⁿ (%) n = 1, 0, -1, -2, …

Значение класса точности прибора приводят в его паспорте, маркируется на его шкале или на корпусе. Для того чтобы различить, какая из погрешностей обозначена в качестве класса точности, используются следующие условные обозначения.

Если форма полосы погрешности прибора принята чисто мультипликативной, то класс точности устанавливают по значению погрешности чувствительности g_s, а обозначаемое на шкале значение класса точности обводится кружком. Например, (0,5) обозначает, что g_s = 0,5%.

Если форма полосы погрешностей прибора принята чисто аддитивной, то нормируют в качестве класса точности значение приведенной погрешностью нуля g₀. Класс точности указывается просто 0,5 что обозначает g₀ = 0,5%.

Если полоса погрешностей содержит и аддитивную и мультипликативную составляющие, то обозначение класса точности в виде дроби, 0,01/0,005 = g_к/g_н указывает, что погрешность прибора нормирована по двучленной формуле с g_к = 0,01% и g_н = 0,005%.
Прогрессирующие погрешности

Прогрессирующими (или дрейфовыми) называются непредсказуемые погрешности, медленно изменяющиеся во времени. Основной причиной появления погрешности является то, что с течением времени в элементах схемы ИК протекают разнообразные процессы старения, его характеристики постоянно изменяются и погрешность возрастает. Поэтому изготовители СИ нормируют гарантированные пределы допускаемой погрешности с 1,5 ¸ 2,5 кратным запасом на старение. Такое превышение пределов допускаемой погрешности над фактическим значением погрешности СИ в момент их выпуска с производства или из ремонта является единственным практическим способом обеспечения долговременной метрологической стабильности средств измерений.

Процесс накопления прогрессирующей погрешности СИ во времени является единообразным для всех СИ: аналоговых и цифровых приборов и измерительных каналов измерительных информационных систем (ИИС). Рассмотрим пример изменения прогрессирующей погрешности для прибора класса точности 0,5 за первые пять лет его эксплуатации. У нового, только что изготовленного прибора, при t = 0 полоса погрешностей располагается симметрично относительно нуля в границах ± 0,1%. Систематическая погрешность отсутствует, так как она устранена благодаря проведенной градуировке шкалы прибора, а случайная погрешность составляет одну пятую часть от нормированного предела g_кл = 0,5%.

Изменение погрешности с возрастом t прибора происходит в виде прогрессирующего смещения и поворота полосы погрешностей, т.е. в виде непрерывного возрастания систематической составляющей погрешности прибора, в то время как размер случайной составляющей определяется шириной полосы погрешностей и остается практически неизменным.