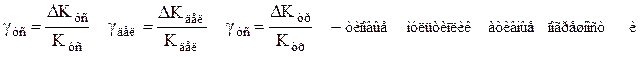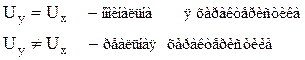Основная и дополнительная погрешности СИ.
- основная погрешность (intrinsic error) - погрешность средства измерений, то есть инструментальная погрешность в нормальных условиях эксплуатации (in reference conditions), - погрешность в рабочих условиях эксплуатации (in normal conditions) - состоит из двух составляющих: основной погрешности и дополнительной погрешности. Основная погрешность средства измерений – это погрешность в условиях, принятых за нормальные, т.е. при нормальных значениях всех величин, влияющих на результат измерения. ГОСТ 8.395 При градуировке приборов все значения влияющих величин могут поддерживаться в узких пределах их изменения, например, окружающая температура (20 ± 5)ºС, напряжение питания U ном ±5%, коэффициент гармоник напряжения питания не более 1%,относительная влажность (65±5%), параметры внешних электрических и магнитных полей и т.д. Такие оговоренные в технической документации условия градуировки принято называть нормальными, а погрешность прибора, возникающую в этих условиях, основной погрешностью. Дополнительная погрешность (complementary error) - составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или ее выхода за пределы нормальной области значений. Дополнительная погрешность возникает при отличии значений влияющих величин от нормальных значений. Влияющая величина (influence quantity) - величина, оказывающая влияние на результаты и на погрешности измерений, но не являющаяся измеряемой. Обычно различают отдельные составляющие дополнительной погрешности, например температурную погрешность, погрешность из-за изменения напряжения питания и т.п. Дополнительные погрешности нормируются указанием коэффициентов влияния, которые показывают, каким образом, сказываются изменения отдельных влияющих величин на изменение показаний ИК
Функции влияния влияющих факторов, как правило, нелинейные, но для простоты вычислений их приближенно считают линейными и возникающие дополнительные погрешности определяют
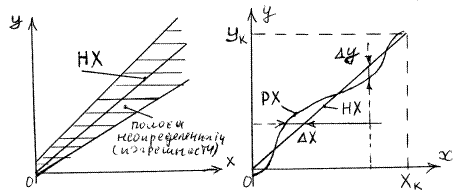
Погрешность прибора в реальных условиях его эксплуатации называется эксплуатационной и складывается из его основной погрешности и всех дополнительных и может быть много больше его основной погрешности. Статические и динамические погрешности. Статическими называют погрешности, не зависящие от скорости изменения измеряемой величины во времени. Динамическими называют погрешности, отсутствующие, когда скорость изменения измеряемой величины во времени близка к нулю, и возрастающие при ее отклонении от нуля. Динамические погрешности можно рассматривать как разновидность дополнительной погрешности, вызванной влияющей величиной в виде скорости изменения во времени самой измеряемой величины. Эти погрешности свойственны как средствам, так и методам измерений. Систематические и случайные погрешности. Систематическая составляющая погрешности, систематическая погрешность) - погрешность, значения которой остаются неизменными при повторных измерениях одной и той же неизменной измеряемой величины в одинаковых условиях. Случайная составляющая погрешности, случайная погрешность - погрешность, значения которой изменяются случайным образом при повторных измерениях одной и той же неизменной измеряемой величины в одинаковых условиях. Систематическими называются погрешности, не изменяющиеся с течением времени или являющиеся не изменяющимися во времени функциями определенных параметров. Основной отличительный признак систематических погрешностей состоит в том, что они могут быть предсказаны и благодаря этому почти полностью устранены введением соответствующих поправок. Опасность постоянных систематических погрешностей заключается в том, что их присутствие чрезвычайно трудно обнаружить, т.к. внешне себя никак не проявляют и могут оставаться незамеченными. Однако, если такие погрешности выявить, например в процессе градуировки ИК, то их можно один раз скорректировать и полностью исключить их влияние. Примером систематических погрешностей второго вида служит большинство дополнительных погрешностей, являющихся не изменяющимися во времени функциями вызывающих их влияющих величин (температур, частот, напряжения и т.п.). Эти погрешности благодаря постоянству во времени функций влияния могут быть предсказаны и скорректированы введением корректирующих цепей или поправок. Прогрессирующими (или дрейфовыми) называются непредсказуемые погрешности, медленно изменяющиеся во времени. Эти погрешности, как правило, вызываются процессами старения тех или иных деталей аппаратуры (разрядкой источников питания, старением резисторов, конденсаторов, аналоговых полупроводниковых элементов). Прогрессирующие погрешности могут быть скорректированы введением поправки лишь в данный момент времени, а далее вновь непредсказуемо возрастают. Поэтому они требуют периодического повторения коррекции. Случайная составляющая погрешности, случайная погрешность - погрешность, значения которой изменяются случайным образом при повторных измерениях одной и той же неизменной измеряемой величины в одинаковых условиях. Случайными погрешностями называют непредсказуемые ни по знаку, ни по размеру погрешности. Причины их возникновения обычно трудно проанализировать. Присутствие случайных погрешностей легко обнаруживается при повторных измерениях в виде некоторого разброса получаемых результатов. Описание случайных погрешностей может быть осуществлено только на основе теории вероятностей и математической статистики. Понятия полосы погрешностей, реальной и номинальной характеристик СИ. Все перечисленные ранее погрешности приводят к тому, что многократно снятые градуировочные характеристики прибора или серии однотипных приборов занимают на графике некоторую полосу. Поэтому в теории измерений используется понятие полосы неопределенности, или полосы погрешностей данного типа прибора, датчика или измерительного канала ИИС. Средняя линия этой полосы принимается за номинальную характеристику или номинальную функцию преобразования приборов этого типа, указывается в паспорте и используется для определения результатов измерения.
Погрешность данного измерительного преобразователя, датчика, прибора или канала ИИС есть разность между реальной и номинальной его характеристиками, т.е. не число, а функция измеряемой величины. Абсолютная, относительная и приведенная погрешности СИ. Понятия абсолютной, относительной и приведенной погрешностей существующими стандартами установлены только для СИ, но их удобно использовать и при характеристике погрешностей результатов измерения. Абсолютная погрешность результата измерений (absolute error) - разность между результатом измерения и истинным значением измеряемой величины, выражается в единицах измеряемой величины. Разность между реальной и номинальной характеристиками в виде
является абсолютной погрешностью, так как она выражаются в единицах величин x или y. Знак абсолютной погрешности принимают положительным, если реальная характеристика проходит выше номинальной. Значение абсолютной погрешности не может быть определено в виде числа из-за того, что истинное значение x измеряемой величины неизвестно. По этой причине результат каждого измерения содержит неустранимую неопределенность значения измеряемой величины, и поэтому на практике может идти речь только об оценке каких-либо характеристик погрешности измерений, но не значений погрешности. Наиболее распространенной характеристикой погрешности является интервал Абсолютная погрешность, однако, сама по себе не является показателем точности измерений, так как одно и то же ее значение, например Dx = 0,01 мм при x = 1000 мм, соответствует высокой точности, а при x = 0,1 мм – низкой. Поэтому для характеристики точности результатов измерения вводится понятие относительной погрешности, выражаемой в относительных единицах или в процентах
Относительная погрешность результата измерений (relative error)- отношение абсолютной погрешности результата измерений к истинному значению измеряемой величины, выражается в относительных единицах или в процентах. Поскольку истинное значение измеряемой величины неизвестно, относительная погрешность вычисляется по отношению к результату измерения. Покажем, что такая замена в большинстве случаев допустима, ибо она приводит к изменению значения погрешности на величину второго порядка малости по сравнению с погрешностью Относительная погрешность является наглядной характеристикой точности результата измерения, но часто не годится для нормирования погрешности СИ, так как при различных значениях x может принимать различные значения, в том числе
Поэтому для указания и нормирования погрешности СИ используется еще одна разновидность погрешности, а именно так называемая приведенная погрешность. Приведенная погрешность определяется как отношение абсолютной погрешности, выраженной в единицах входной или выходной величин, к протяженности диапазона изменения соответственно входной или выходной величины прибора или преобразователя и выражается в относительных единицах или в процентах
Основное отличие приведеннойпогрешности от относительной погрешности состоит в том, что абсолютная погрешность относится не к переменной текущей величине, а к постоянной величине протяженности диапазона, поэтому для всего диапазона измерения ее можно выразить одним числом, например максимальным значением. Приведенную погрешность удобно использовать для нормирования свойств многих многопредельных СИ, т.к. она может иметь одно и то же значение для всех диапазонов СИ. Абсолютные и относительные погрешности могут служить характеристиками качества результатов измерений и средств измерений. Приведенные погрешности являются характеристикой только инструментальной погрешности средств измерений.
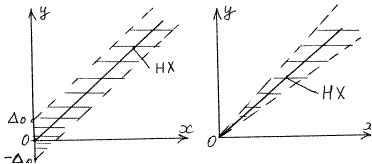
Аддитивные и мультипликативные погрешности. Эти термины служат для описания формы границ полосы погрешностей СИ. В том случае, когда полоса погрешностей ограничена двумя параллельными друг другу линиями, абсолютная погрешность СИ во всем его диапазоне измерений ограничена постоянным пределом ±D0, не зависящим от текущего значения x. Такая погрешность называется аддитивной, т.е. получаемой путем сложения, или погрешностью нуля. Это понятие одинаково применимо как к случайным, так и к систематическим погрешностям.
Примерами систематических аддитивных погрешностей являются погрешности от неточной установки прибора на нуль перед измерением, от термо-ЭДС в цепях постоянного тока и т.п. Примерами случайных аддитивных погрешностей являются погрешность от наводки переменной ЭДС на вход прибора, погрешности от тепловых шумов на входе канала. Если ширина полосы погрешностей возрастает пропорционально росту входной величины x, а при x = 0 также равна нулю, то такая погрешность называется мультипликативной, то есть получаемой путем умножения, или погрешностью чувствительности вне зависимости от того, является ли погрешность случайной или систематической. Причинами возникновения мультипликативных погрешностей могут быть: изменение коэффициента усиления усилителя, отклонение от номинального значения коэффициента деления резистивного делителя или коэффициента трансформации измерительного трансформатора
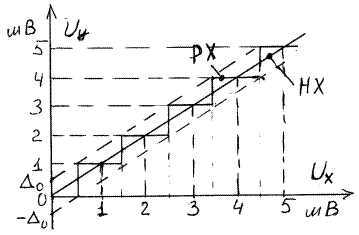
Погрешность квантования. Это специфическая разновидность погрешности, возникающая в цифровых приборах, АЦП и ЦАП. Цифровой вольтметр, имеющий трехразрядный цифровой индикатор и диапазон измерения (0 ¸ 999) мВ, при изменении входного напряжения Ux в пределах от 0 до 1В не может дать других показаний, кроме дискретных значений Uy = 0-1-2-3-4-5-…-999 мВ. Следовательно, правильно отрегулированный прибор при возрастании Ux от 0 до 0,5мВ прибор показывает Uy = 0. При превышении значения 0,5мВ прибор дает показание Uy = 1 и сохраняет его до Ux = 1,5мВ и т.д. Поэтому, хотя его номинальной характеристикой мы считаем прямую, его реальная характеристика представляет собой ступенчатую кривую
Текущая разность номинальной и реальной характеристик цифрового прибора и составляет погрешность квантования. Границы полосы погрешности квантования сохраняют на всем протяжении постоянную ширину, т.е. погрешность является аддитивной или погрешностью нуля.
Максимальное значение погрешности составляет половину младшего разряда СИ, в данном случае ± 0,5мВ.
Измеряемая величина Ux случайным образом может принимать любые промежуточные значения, следовательно, и погрешность квантования также случайным образом принимает значения в интервале от +D0 до -D0. Поэтому погрешность квантования является инструментальной случайной аддитивной статической погрешностью, так как не зависит ни от текущего значения результата измерения величины x, ни от скорости изменения x во времени.
|

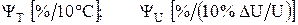
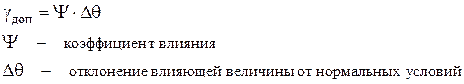
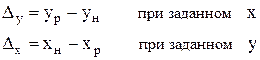
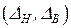 , ограниченный предельными или предельно допускаемыми значениями. Обычно принимают
, ограниченный предельными или предельно допускаемыми значениями. Обычно принимают 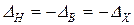 , то ест считают этот интервал симметричным относительно нуля:
, то ест считают этот интервал симметричным относительно нуля: 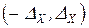 .
.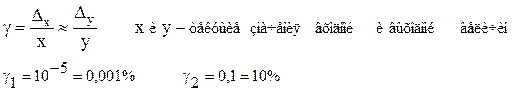
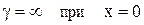 - возможно
- возможно