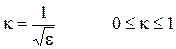Вероятностные оценки ширины распределения

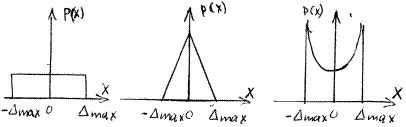
Для оценки величины разброса случайных погрешностей относительно центра, т. е. ширины распределения, на практике используют несколько способов, приводящих к разным результатам.

Предельная, или максимальная, оценка случайной погрешности. Она теоретически правомерна только для ограниченных распределений, у которых существуют максимальные пределы ±D_max, ограничивающие с обеих сторон возможные значения случайной величины (равномерного, трапецеидального, треугольного, арксинусоидального).

Однакомаксимальная оценка имеет ряд недостатков, препятствующих её практическому применению:

- ограниченные распределения являются лишь теоретической идеализацией реальных распределений погрешностей, обычно, не имеющих четко выраженных границ и указание для реальных распределений предельных или максимальных значений, неправомерно

- оценка не устойчива, т.к. при увеличении числа отсчётов n оценка будет возрастать

- максимальные оценки нельзя суммировать при определении результирующей погрешности, т.к. оценка суммы не равна сумме оценок

 

Второй центральный момент называется дисперсией случайной величины.

Дисперсия случайной величины есть характеристика рассеивания, или разброса отдельных значений случайной величины около ее математического ожидания,т.е. от центра распределения. Само слово дисперсия означает рассеивание.

Дисперсия имеет размерность квадрата случайной величины и характеризует мощность рассеяния относительно постоянной составляющей. Поэтому для более наглядной характеристики самого рассеяния берут положительное значение корня квадратного из дисперсии. Оно характеризуют действующее значение рассеяния, которое называется среднеквадратическим отклонением (с.к.о.) s и имеет размерность самой случайной величины.

Среднее квадратическое отклонение s случайной величины (с. к. о.) - положительное значение квадратного корня из ее дисперсии

Для определения оценки дисперсии и оценки с.к.о. по экспериментальным данным

Основным достоинством оценки разброса случайных величин средним квадратическим значением s является возможность определения результирующей дисперсии или с.к.о. суммы величин независимо от законов распределения каждой суммируемой величины и суммарного закона распределения. Достоверность такой оценки повышается с увеличением числа n.

Таким образом, для того чтобы отдельные составляющие погрешности средств измерений можно было суммировать расчетным путем, они должны быть предварительно представлены своими средними квадратическими значениями s, а не «максимальными» D_max или квантильными D_p значениями. При этом открывается возможность расчетным путем складывать любое число составляющих погрешности, что необходимо при анализе точности косвенных измерений или сложных измерительных устройств.

Оценка погрешностей с использованием с.к.о. имеет и недостатки:

1. С.к.о. существует не для всех законов распределения, например не существует для распределения Коши.
2. Для различных законов распределения значению s соответствует различная доверительная вероятность P_д. - примеры!!!

 

Квантильные оценки случайной погрешности. Площадь, заключенная под кривой плотности распределения согласно правилу нормирования, равна единице, т. е. отражает вероятность всех возможных событий, равную 100%.

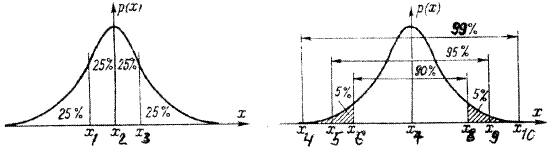
Эту площадь можно разделить на некоторые части вертикальными линиями, координаты которых называют квантилями. Медиана x = x₂ и x = x₇ – это 50%-ная квантиль, так как она делит площадь под кривой распределения p(x) на две равные части. Квантиль x = x₁ называют 25%-ной квантилью, так как площадь под кривой распределения p(x) слева от нее составляет 25% всей площади, а справа – 75% площади. Квантиль x = x₃ называют 75%-ной квантилью, так как площадь под кривой распределения p(x) слева от нее составляет 75% всей площади, а справа – 25% площади.Между x = x₁ и x = x₃, т. е. между 25%-той и 75%-ной квантилями, которые принято называть сгибами данного распределения, заключено 50 % всех возможных значений погрешности, а остальные 50% лежат вне этого промежутка.

Квантили x₄ = x_0,005; x₅ = x_0,025; x₆ = x_0,05; x₈ = x_0,95; x₉ = x_0,975; x₁₀ = x_0,995 – это соответственно 0,5%; 2,5%; 5%; 95%; 97,5%; 99,5%-ная квантили, так как площадь под кривой слева от них составляет соответствующий процент всей площади под кривой распределения p(x).

Интервал значений случайной величины x между двумя симметричными квантилями называют интерквантильным промежутком.

Интервал между x_0,05 и x_0,95; охватывает 90% всех возможных значений случайной величины x и называется интерквантильным промежутком с 90%-ной вероятностью. Следовательно, вероятность попадания случайной величины в этот промежуток составляет 90%. Протяженность соответствующего интерквантильного промежутка

На основании такого подхода вводится понятие квантильных оценок погрешности, с заданной доверительной вероятностью P_д.

Квантильным значением погрешности с заданной доверительной вероятностью P_д, называют границы интервала неопределенности, на протяжении которого встречается P_д всех значений погрешности, а (1 - P_д ) общего числа значений погрешности остаются за границами этого интервала

В случае если закон распределения погрешности симметричный, т.е. отсутствует систематическая составляющая, границы квантильной погрешности симметричны

Квантильное значение случайной погрешности есть ее максимальное значение с указанной доверительной вероятностью P_д, причем часть реализаций погрешности с вероятностью (1 - P_д) может быть и больше указанного значения погрешности.

Так как квантили, ограничивающие интервал погрешности, могут быть выбраны различными, то при сообщении такой оценки должно одновременно обязательно указываться значение принятой доверительной вероятности P_д. Обозначение квантильной погрешности снабжают индексом, численно равным принятой доверительной вероятности

Определение квантильного значения погрешности по экспериментальным данным Достоинство доверительного значения погрешности состоит в том, что оно может быть достаточно просто оценено прямо по экспериментальным данным. Пусть проведена серия из n измерений, в результате которых получено n результатов x каждый с погрешностью D. Из полученных n случайных погрешностей составляют вариационный ряд, располагая их в порядке возрастания.

Далее считают, что каждый член вариационного ряда из наблюдавшихся значений погрешности D^k является оценкой соответствующих квантилей, которые делят весь интервал возможных вероятностей (от 0 до 1) на n + 1 частей с равными значениями вероятности. Следовательно, вероятности попадания значений погрешности в каждый из интервалов предполагаются одинаковыми, равными 1/(n + 1).

Практическое определение квантильной погрешности D_p сводится к тому, что из всех полученных отсчетов отбрасываются наиболее удаленные от центра, следовательно, самые ненадежные отсчеты, а по остальным отсчётам определяют границы погрешности.

Следует иметь в виду, что по ограниченному ряду экспериментальных данных получают не точные квантильные значения погрешностей, а лишь их приближенные значения – оценки. Вариационный ряд из n членов определяет границы n + 1 интервалов, вероятность попаданий в которые принята одинаковой. При отбрасывании лишь крайних или пустых интервалов, не содержащих отсчётов, оценка погрешности может быть определена с доверительной вероятностью, не большей

При небольших объемах выборки n достоверность оценки D_p, найденной таким путем, может быть мала. Для определения оценки D_p с большей достоверностью с каждого из концов вариационного ряда должны быть отброшены не только пустые интервалы (-¥, D¹) и (Dⁿ, +¥;), но и какое-то число фактических отсчетов. Располагая рядом из n отсчетов и отбрасывая с каждого из концов ряда по n_отбр отсчетов, можно определить оценку D_p с доверительной вероятностью, не большей

Число отсчетов n, необходимое для определения по экспериментальным данным квантильной погрешности D_p с заданной доверительной вероятностью P_д, не менее

Для различных значений P_д и n_отбр = 1, 2 и 5

Достоверность квантильных оценок резко повышается с понижением значений P_д, а при постоянном значении P_д – с ростом числа отсчетов n. Поэтому квантильные оценки с большими доверительными вероятностями P_д могут быть найдены только при большом числе отсчетов.

По экспериментальным данным легко определить значение оценки квантильной погрешности D_p с высокой доверительной вероятностью P_д в случае, когда возможна автоматизация проведения эксперимента. Причем объем выборки n, лишь обеспечивает выполнение неравенства для P_д. Так, при выборке объемом в n = 80 и n_отбр=1 доверительная вероятность не может быть большей, чем 0,95, но нет оснований утверждать, что она равна 0,95.

Квантильные оценки случайных погрешностей имеют ряд достоинств.

1. Простота практического определения значения погрешности.

2. Устойчивость оценки. Если при переменном значении n отбрасывается постоянная относительная доля всех отсчетов, то определяемое по крайним членам оставшегося вариационного ряда значение D_p с ростом длины n серии отсчетов не возрастает, а стабилизируется и оказывается тем более устойчивым, чем больше объем выборки n.

Этим квантильная оценка D_p выгодно отличается от максимальной оценки D_m, зависящей от объема выборки n.

3. Оценка существует для всех законов распределения, в отличие, например, от дисперсии.

Основным недостатком квантильной погрешности D_p при произвольно выбираемых значениях P_д, как и «максимальной» погрешности D_m, является невозможность их суммирования, так как доверительный интервал суммы не равен сумме доверительных интервалов слагаемых.

Математическое ожидание m_x, дисперсия D_x или среднеквадратическое отклонение s_x - наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности.

Для более подробного описания распределения применяют моменты высших порядков, в первую очередь третий и четвертый центральные моменты.

Третий центральный момент m₃ характеризует асимметрию или скошенность распределения: когда один спад – крутой, а другой – пологий. Для симметричных относительно центра распределений он равен нулю.

Если распределение симметрично относительно математического ожидания, то все моменты нечетного порядка равны нулю.

При симметричном относительно m_x законе распределения и нечетном k каждому положительному слагаемому в сумме соответствует равное ему по абсолютной величине отрицательное слагаемое, так что вся сумма равна нулю. То же, справедливо и для интеграла, который равен нулю, как интеграл в симметричных пределах от нечетной функции.

Третий момент имеет размерность куба случайной величины, поэтому для относительной характеристики асимметрии используют безразмерный коэффициент асимметрии s, равный третьему моменту, деленному на куб с.к.о.

Два асимметричных распределения: одно из них (кривая I) имеет положительную асимметрию; другое (кривая II) — отрицательную.

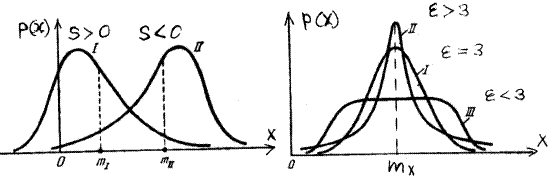
Четвертый центральный момент m₄ характеризует протяженность распределения. Его относительное значение e называется эксцессом распределения.

Для широко распространенного в природе нормального закона распределения эксцесс равен 3 (кривая I). У кривых, более узких, имеющих более медленный спад при увеличении x по сравнению с кривой нормального распределения, значение e > 3, (кривая II); у кривых более протяженных у центра распределения, спадающих быстрее при увеличении x, чем нормальное распределение или ограниченных по x, значение эксцесса e < 3 (кривая III).

e_{равномер} e_{треугол} e_норм e_коши

1,8 2,4 3 ¥;

Для разных законов распределения значение e может меняться от 1 до ¥;. Поэтому для классификации распределений по их форме удобнее использовать функцию k, которую называют контрэксцессом, изменяющуюся для любых распределений лишь в пределах 0 £ k £ 1.

Математическое ожидание, мода, медиана, начальные и центральные моменты и, в частности, дисперсия, среднеквадратическое отклонение, асимметрия и эксцесс представляют собой наиболее употребительные числовые характеристики случайных величин.

Во многих задачах практики полная характеристика случайной величины — закон распределения не может быть получена. В этих случаях случайная величина может быть приблизительно описана с помощью числовых характеристик, каждая из которых выражает какое-либо характерное свойство распределения.
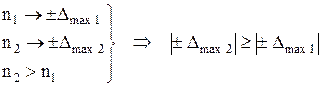
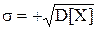
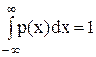
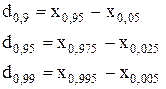
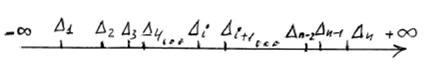
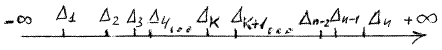
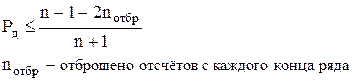
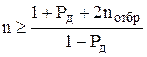
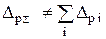
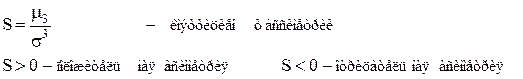