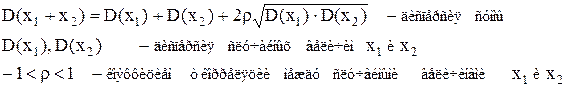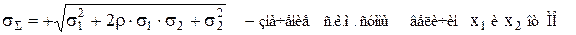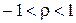Суммирование дисперсии и с.к.о. коррелированных и некоррелированных погрешностей

Часто используемыми числовыми оценками законов распределения является дисперсия или с.к.о. - среднеквадратическое отклонение, в качестве которого берут положительное значение корня квадратного из дисперсии

Эти оценки определяют разброс случайной величины вокруг МО.

Согласно теории вероятностей дисперсия суммы величин x₁ и x₂

Коэффициент корреляции определяет вероятностную связь между случайными величинами, причем, чем теснее связаны эти величины, тем больше значение модуля r.

Среднеквадратическое отклонение суммы величин x₁ и x₂ от ее математического ожидания

Возможны три крайних случая:

1. Величины x₁ и x₂ между собой некоррелированы. В таком случае берут корень квадратный из суммы квадратов с.к.о., причем формула справедлива для любого числа слагаемых

2. Величины x₁ и x₂ между собой жестко и положительно коррелированны. В таком случае отклонение Dx₂ принимает значения, лишь строго пропорциональные отклонению Dx₁. Всякое положительное отклонение + Dx₁ сопровождается также положительным отклонением + Dx₂. Результирующее отклонение D(x₁+x₂) складывается как Dx₁ + Dx₂. Значение коэффициента корреляции в таком случае r = +1.

3. Величины x₁ и x₂ между собой жестко и отрицательно коррелированны. В таком случае при возрастании x₁ значение x₂, наоборот, линейно убывает. Значение коэффициента корреляции в таком случае r = -1.

Если в результирующей погрешности одновременно присутствуют жестко положительно и жестко отрицательно коррелированные составляющие, то их нужно предварительно просуммировать по отдельности и потом вычесть

Таким образом, оценки жестко коррелированных погрешностей при r = ±1 должны суммироваться алгебраически, с учетом их знаков. На практике коэффициент корреляции находится в пределах

и определить его реальное значение обычно не представляется возможным. Поэтому, при практическом суммировании погрешностей, часто полагают, что погрешности не коррелированны, если взаимозависимость между ними явно не просматривается. Если взаимозависимость между погрешностями явно видна, то считают их жестко положительно или отрицательно коррелированными.