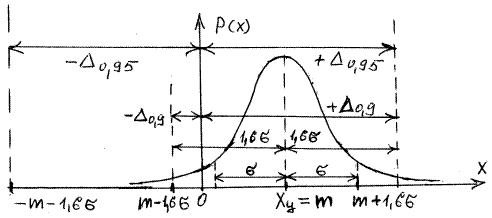
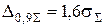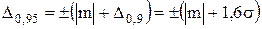Суммирование квантильных погрешностей
Квантильное значение погрешности ±Dp, определяет с заданной доверительной вероятностью Pд допустимые максимальные границы погрешности. Достоинство квантильного значения погрешности состоит в том, что оно существует для любых законов распределений (в отличие от среднеквадратического и энтропийного значений). Основной недостаток квантильного значения погрешности состоит в невозможности его расчетного определения для суммы нескольких погрешностей по известным значениям составляющих
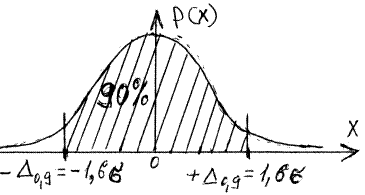
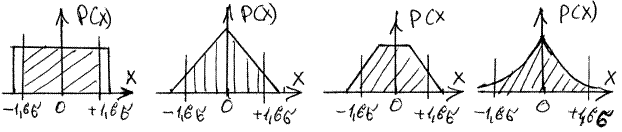
Однако из этого правила есть важное исключение справедливое для широкого класса симметричных распределений случайных погрешностей: равномерного, треугольного, трапецеидального, нормального, экспоненциального и многих двухмодальных. Интегральные кривые таких законов в районе 0,05-й и 0,95-й квантилей – X0,05 и X0,95 пересекаются между собой в очень узком интервале значений x/s = 1,6 ± 0,05. Поэтому с погрешностью 0,05s можно считать, что 0,05-я и 0,95-я квантили для любых из этих распределений могут быть определены как
Значение квантильной погрешности, определенное как
для любых из этих распределений является погрешностью с 90%-ной доверительной вероятностью. В дифференциальном законе распределения границы погрешности ± D0,9 означают, что 90% площади заключенной под кривой распределения находятся между этими границами.
Так как при суммировании погрешностей, результирующее распределение принадлежит классу исходных распределений, то и для него справедливо соотношение
Это обстоятельство позволяет использовать простой метод суммирования квантильных погрешностей. Так, если заданы значения суммируемых составляющих, и они не коррелированны между собой
Квантильные оценки погрешности с доверительной вероятностью Pд = 0,9 можно суммировать аналогично с.к.о. погрешности. Таким образом, предпочтительным значением доверительной вероятности при нормировании случайных погрешностей является вероятность Pд = 0,9. Такое значение является предпочтительным ещё и потому, что оценка D0,9 определяется с гораздо большей точностью, чем, например, D0,95 или D0,99. Используя границы квантильной погрешности ±Dp, необходимо иметь в виду, что эти границы располагаются симметрично относительно нуля лишь при отсутствии у измерительного канала систематической составляющей погрешности m. Если m ≠ 0, то границы погрешности оказываются несимметричными, т.к. центр распределения погрешности будет смещен относительно начала координат x = 0. В качестве систематической составляющей погрешности принимают центр распределения m = Xц, который часто определяют как МО распределения. При использовании экспериментальных данных за оценку центра распределения Xц обычно принимают среднее арифметическое. Например, если случайная составляющая относительной погрешности gp = ± 0,3%, а систематическая составляющая относительной погрешности gm = + 0,2%, то одна граница оказывается равной g-p = -0,3 + 0,2 = -0,1%, а другая g+p = + 0,3 + 0,2 = + 0,5%. Пользоваться при дальнейших расчетах такими несимметричными границами погрешностей крайне неудобно. Поэтому на практике всегда проводят симметрирование границ погрешностей и окончательно указывают симметричные границы, равные по модулю большей из несимметричных границ. Вместо пределов gp = (- 0,1 ¸ + 0,5)% указывают пределы gp = ± 0,5%. Вероятность выхода погрешности за такие симметричные границы, в два раза меньше, так как такой выход происходит практически только с одной стороны, а не с обеих. В результате, если g0,9 = ± 0,3% была определена с Pд = 0,9, то g0,95 = ± 0,5% есть погрешность с доверительной вероятностью Pд = 0,95. Таким образом, при наличии относительно большой систематической составляющей m ³ 0,5s» 0,31D0,9 результирующая погрешность просто определяется через m и оценку D0,9 случайной составляющей
В тех случаях, когда закон распределения погрешностей близок к нормальному распределению, для определения симметричных границ доверительной погрешности с доверительной вероятностью Pд = 0,95 (при m = 0) можно использовать теоретическое соотношение для нормального распределения D0,95 = 1,96s.
Практические правила расчетного суммирования составляющих результирующей погрешности 1. Отдельные составляющие погрешности могут быть коррелированны между собой. Корреляционные связи составляющих учитывают используя для характеристики суммируемых составляющих погрешности их числовые оценки в виде среднего квадратического значения и коэффициентов взаимной корреляции. Коррелированные составляющие погрешности могут принадлежать различным преобразователям измерительного канала. Поэтому исходными данными для более точного расчета должны служить оценки именно всех отдельных составляющих погрешности, а не оценки некоторых суммарных погрешностей отдельных преобразователей. 2. Так как суммировать с учетом корреляционных связей можно лишь средние квадратические значения составляющих погрешности, то для каждой составляющей должны быть по исходным данным найдены ее средние квадратические значения. 3. Числовые характеристики законов распределения могут изменяться в диапазоне изменения входной величины. Это требует разделения составляющих погрешности на аддитивные и мультипликативные составляющие. Их суммируют раздельно для определения аддитивной и мультипликативной составляющих результирующей погрешности 4. Должны быть выделены группы сильно коррелированных между собой составляющих погрешности и внутри этих групп произведено алгебраическое суммирование. К ним, как правило, относят погрешности, вызванные одной общей причиной (температурная погрешность), когда тесные корреляционные связи определяются логически, и для них принимают r = ±1. Погрешности же, между которыми такие взаимосвязи не обнаруживаются, относят к некоррелированным погрешностям и для них принимают r = 0. 5. После того, как все группы сильно коррелированных погрешностей выделены и внутри их произведено алгебраическое суммирование, суммарные по группам и оставшиеся вне групп погрешности можно считать уже некоррелированными и складывать по правилу
Для определения с.к.о. погрешности sнS в начале диапазона измерений при x = 0 складываются лишь аддитивные составляющие, а для определения с.к.о. sкS в конце диапазона измерений – все суммируемые составляющие. 6. Допустимо пренебрегать малыми составляющими при суммировании погрешностей. Могут быть опущены: одна малая составляющая, если она в 5 раз меньше наибольшей из суммируемых составляющих, две составляющие, если они в 6 раз меньше, три составляющие, если они в 7 раз меньше, и четыре, если они в 8 раз меньше наибольшей. Но делать такое заключение можно только после суммирования коррелированных составляющих. 7. При суммировании случайных величин законы их распределения резко деформируются. Такая деформация не может быть учтена при использовании с.к.о. для оценки погрешности, так как эта оценка не отражает деформации формы результирующих законов распределения. Таким образом, находятся лишь средние квадратические значения аддитивной и мультипликативной составляющих результирующей погрешности, которые не учитывают деформации законов распределения при образовании композиций, и остаются неизвестными параметры формы закона распределения результирующей погрешности. 8. Для перехода от с.к.о. погрешности к энтропийному или доверительному значениям должно быть тем или иным путем вынесено суждение о форме закона распределения результирующей погрешности и тем самым выбрано значение энтропийного коэффициента kS или квантильного множителя tS
|