Общие критерии термодинамической устойчивости
При рассмотрении условий равновесия можно исходить из интегральной формы второго начала термодинамики
S 2 – S 1 ≥
Пусть закрытая система помещена в термостат с постоянной температурой. Тогда неравенство принимает вид
S 2 – S 1 ≥ Q / Te.
Из первого начала термодинамики для закрытых систем
Q = U 2 – U 1 – A '
(здесь A ' – работа внешних сил), так что
S 2 – S 1 ≥ (U 2 – U 1 – A ')/ Te. (53.2)
Рассматриваются два случая. Первый, когда объем системы постоянный (V = const), работа внешних сил отсутствует (A ' = 0). Тогда неравенство (53.2) принимает вид
U 2 – Te S 2 ≤ U 1 – Te S 1.
Если ввести функцию Y = U – Te S, то данное неравенство можно переписать следующим образом:
Y 2 ≤ Y 1.
Таким образом, неравновесные процессы в системе идут с уменьшением функции Y и прекращаются по достижении этой функцией минимума. На рис. 21 в пространстве переменных S, V, Y сплошная кривая в плоскости V = const дает равновесные состояния, определяемые функцией Y; пунктиром изображен переход из начального состояния 1 в конечное состояние 2.
Условия устойчивого равновесия системы в конечном состоянии будут
δ Y = 0 и δ2 Y > 0. (53.3)
Если в качестве независимых переменных выбрать энтропию и объем (на рис. 21 функция Y изображена в этих переменных, они естественные переменные для внутренней энергии), то
δ Y = δ U – Te δ S = ((¶ U /¶ S) V – Te)δ S + (¶ U /¶ V) S δ V.
Но δ V = 0, а (¶ U /¶ S) V = T, поэтому
δ Y = (T – Te)δ S = 0,
и так как вариация δ S отлична от нуля (она задается), то условие равновесия (53.3) приводит к равенству
T = Te.
Если отклонение от равновесного состояния мало, то функция Y совпадает со свободной энергией и минимум первой из них означает минимум и второй. Это согласуется с приведенной на с. 111 таблицей. Вторая вариация функции Y равна
δ2 Y = (¶2 Y / ¶ S 2) V δ S 2 = (¶2 U / ¶ S 2) V δ S 2 = (¶ T / ¶ S) V δ S 2.
В силу условий (53.3),
δ2 Y = (¶ T / ¶ S) V δ S 2 > 0,
откуда
(¶ T /¶ S) V > 0, или cV > 0. (53.4)
Это важное следствие теории устойчивости термодинамических систем. Во втором случае пусть поддерживается постоянным давление термостата pe. Тогда работа над системой равна
A ' = pe (V 1 – V 2),
и неравенство (53.2) переходит в
U 2 – Te S 2 + pe V 2 ≤ U 1 – Te S 1 + pe V 1
или, если ввести функцию Z = U – Te S + pe V, то в
Z 2 ≤ Z 1.
Таким образом, все самопроизвольные процессы в системе могут идти только в сторону уменьшения функции Z. Поверхность Z (S, V) в окрестности конечного равновесного состояния имеет форму параболоида (рис. 22, пунктиром показан неравновесный переход из начального состояния 1 в конечное состояние 2). Функция Z в конечном равновесном состоянии имеет минимум. Условиями устойчивости равновесия будут соотношения
δ Z = 0 и δ2 Z > 0. (53.5)
Пусть теперь состояние системы претерпевает виртуальное смещение, определяемое величинами δ S иδ V (по-прежнему S и V независимые переменные). В таком случае
δ Z = δ U (S, V) – Te δ S + pe δ V.
Так как (¶ U /¶ S) V = T и (¶ U / ¶ V) S = – p, то
δ Z = (T – Te)δ S + (– p + pe)δ V.
По условию (53.5) в состоянии равновесия δ Z = 0. Отсюда следует, что температура и давление системы в равновесном состоянии равны соответствующим значениям для окружающей среды, т. е.
T = Te, p = pe.
Условием устойчивости этого состояния является положительное значение второй вариации функции Z (53.5):
δ2 Z > 0, или δ T × δ S – δ p × δ V > 0. (53.6)
В последней форме записи неравенства (53.5) все вариации равноправны. В качестве независимых переменных можно выбрать теперь температуру и объем (энтропия и давление будут функциями этих переменных). Тогда неравенство перепишется следующим образом:
(¶ S / ¶ T) V δ T 2 + (¶ S / ¶ V) T δ T δ V – (¶ p / ¶ T) V δ T δ V – (¶ p / ¶ V) T δ V 2 > 0.
Если использовать соотношение Максвелла (¶ S / ¶ V) T = (¶ p / ¶ T) V, то условие устойчивости равновесия примет окончательный вид:
cV / T × δ T 2 – (¶ p / ¶ V) T δ V 2 > 0.
Из него следует, что
cV > 0 и (¶ p / ¶ V) T < 0. (53.7)
Эти выводы теории устойчивости неоднократно использовались раньше. Здесь же нелишним будет сказать, что при малых вариациях функцию Z можно заменить потенциалом Гиббса и условие устойчивости равновесия примет вид
δ G = 0 и δ2 G > 0. 54. Принцип Ле-Шателье–Брауна
Условия устойчивости равновесия термодинамических систем приводят к тому, что внешнее воздействие, выводящее систему из состояния равновесия, вызывает в этой системе процессы, которые ослабляют это воздействие. Это положение было установлено французским ученым Ле-Шателье в 1884 г. и обосновано немецким физиком Брауном в 1887 г. Называется оно принципом Ле-Шателье– Брауна. Этот принцип был сформулирован как обобщение известного из электродинамики правила Ленца, в результате рассмотрения большого числа примеров. Принцип Ле-Шателье–Брауна позволяет предсказать направление, в котором под влиянием внешнего воздействия будет протекать процесс в системе. Пример 1. Рассматривается система, находящаяся в термостате. Пусть в некоторый момент времени изменяется давление на нее. Это вызовет изменение объема и температуры. Мерой воздействия является производная ¶ V /¶ p. В первый момент благодаря внезапности изменения давления процесс протекает адиабатически и внешнее воздействие определяется производной (¶ V /¶ p) S. По мере приближения к равновесию температура стремится к первоначальному значению (температуре термостата). Воздействие будет определяться уже производной (¶ V /¶ p) T. По принципу Ле-Шателье–Брауна в результате этого перехода воздействие ослабляется, т. е. должно быть
(¶ V / ¶ p) T < (¶ V / ¶ p) S.
Это неравенство было доказано раньше при использовании условия cp > cV > 0. Пример 2. Если смеси льда и воды сообщить некоторое количество теплоты, лед начнет таять и повышения температуры не произойдет. Пример 3. Для соли, находящейся в насыщенном растворе, повышение температуры вызовет растворение, если оно сопровождается охлаждением; иначе происходит выпадение кристаллов. Принцип Ле-Шателье–Брауна не применим к процессам, переводящим систему в более устойчивое состояние, например к взрывам.
|

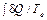 . (53.1)
. (53.1)




