Условие фазового равновесия
Условие фазового равновесия можно получить, исходя из общей теории термодинамической устойчивости. С этой целью рассматриваются две системы, находящиеся в термодинамическом контакте. В зависимости от природы контакта возможны следующие условия равновесия: 1) механическое взаимодействие дает
p 1 = p 2 (56.1)
(при отсутствии других поверхностных сил); 2) тепловое взаимодействие приводит к условию
T 1 = T 2; (56.2)
3) материальное взаимодействие (обмен частицами вещества) дает
μ1 = μ2. (56.3)
Для доказательства условий (56.1)–(56.3) полная система, состоящая из двух данных систем, считается изолированной. Условием ее равновесия является равенство
S 1 + S 2 = max. (56.4)
Имеются дополнительные условия
U 1 + U 2 = const, V 1 + V 2 = const, Nj (1) + Nj (2) = const j = 1, 2,... (56.5)
Эти условия варьируются
δ S 1 + δ S 2 = 0; (56.6)
δ U 1 + δ U 2 = 0, δ V 1 + δ V 2 = 0, δ Nj (1) + δ Nj (2) = 0. (56.7)
Основное уравнение термодинамики для каждой подсистемы имеет вид
T 1 δ S 1 = δ U 1 + p 1 δ V 1 –
T 2 δ S 2 = δ U 2 + p 2 δ V 2 –
Если из этих уравнений выразить величины δ S 1 и δ S 2 и подставить их в соотношение (56.6), то оно примет вид
δ U 1 / T 1 + p 1 / T 1 × δ V 1 –
+ δ U 2 / T 2 + p 2 / T 2 × δ V 2 –
Последнее равенство с учетом условий (56.7) приводится к виду
(1 / T 1 – 1 / T 2)δ U 1 + (p 1 / T 1 – p 2 / T 2)δ V 1 –
Здесь вариации величин, относящихся к первой системе, считаются независимыми. В силу их произвольности из полученного равенства следуют условия равновесия (56.1)–(56.3). Если две системы – это просто две фазы одного и того же вещества (например, вода и ее пар), то три условия равновесия можно записать в виде одного уравнения
μ1(T, p) = μ2(T, p). (56.10)
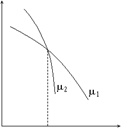
Это условие фазового равновесия. Оно показывает, что при равновесии двух фаз какого-либо вещества давление является функцией температуры (параметры T и p перестают быть независимыми). На (p, T) – плоскости (рис. 23) уравнение (56.10) представляет кривую, называемую кривой фазового равновесия. Выше или ниже этой кривой устойчивой является та фаза, у которой меньше термодинамический потенциал Гиббса (условие устойчивого равновесия – его минимум) и соответственно меньше химический потенциал. Если, например, одной из фаз является жидкость, а другая фаза – пар, то область на плоскости p, T выше кривой равновесия отвечает жидкой фазе, а ниже – газообразной.
|

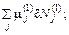 (56.8)
(56.8)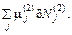 (56.9)
(56.9)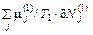 +
+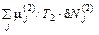 = 0.
= 0. = 0.
= 0.