Равновесие между паром и конденсированной фазой
При исследовании равновесия между конденсированной фазой (жидкостью, кристаллом) и паром можно считать, что молярный объем пара много больше, чем молярный объем конденсированной фазы, и последним пренебречь. Уравнение Клапейрона–Клаузиуса в этом случае примет вид
dp / dT = λ / (TVп).
Если при этом пар является достаточно разреженным, так что его можно считать идеальным газом, то Vп = RT / p и
dp / p = λ dT / (RT 2). (59.1)
Зависимость λ от T может быть найдена приемом, аналогичным тому, что применялся при получении уравнения (58.1). Дифференцирование по T выражения (57.1) для λ дает
d λ / dT = ∆ S + T (¶∆ S / ¶ T) p + T (¶∆ S / ¶ p) Tdp / dT =
= ∆ S + ∆ cp – T (¶∆ V / ¶ T) p dp / dT.
С учетом уравнения Клапейрона–Клаузиуса (58.1) и того, что ∆ V» Vп, а пар – идеальный газ,
d λ / dT = ∆ S + ∆ cp – T (R / p) ∆ S / Vп = ∆ cp.
Таким образом, скрытая теплота перехода при некоторой температуре T равна
λ = λ0 +
Основным членом в выражении для λ (59.2) является первое слагаемое; второе добавляет слабую зависимость λ от T. Если λ приближенно считать постоянной, то интегрирование (59.1) приводит к
ln (p / p 0) = λ/ R ×(T 0–1 – T –1) и p = A exp(– λ /(RT)).
Несложно проинтегрировать уравнение (59.1) и с учетом второго члена, когда ∆ cp = const, при этом получится
ln (p / p 0) = λ/ R ×(T 0–1 – T –1) + ∆ cp / R × ln (T / T 0),
или ln p = A – B / T + C ln T.
Это уравнение было получено Кирхгофом и широко используется для обработки экспериментальных данных.
|
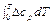. (59.2)
