Третье начало термодинамики (теорема Нернста)
На основании многих опытов, проводившихся при низких температурах, сформулировано третье начало термодинамики. Этот закон был открыт в 1906 г. Нернстом, а потому получил название теоремы Нернста. Однако современная формулировка теоремы принадлежит в основном Планку. Энтропия химически однородного тела конечной плотности при стремлении температуры к абсолютному нулю стремится к предельному значению, не зависящему от давления, плотности или фазы:
В этой формулировке содержатся два утверждения. Первое состоит в том, что при приближении к абсолютному нулю температуры энтропия системы стремится к определенному конечному значению. Это нетривиальное утверждение, так как заранее не очевидно, что при T → 0 интеграл Вторая часть теоремы утверждает, что все процессы при абсолютном нуле температуры, переводящие систему из одного равновесного состояния в другое, происходят без изменения энтропии, т. е. предел (50.1) не зависит от того, в каком конечном состоянии окажется система. Из трактовки энтропии как меры беспорядка следует, что энтропия при абсолютном нуле температуры имеет минимальное значение. Удобно поэтому принять это состояние за начальное (значение S 0 положить равным нулю) и от него вести отсчет. Тогда энтропия произвольного состояния определяется однозначным образом. Из теоремы Нернста вытекает ряд важных результатов: 1. Недостижимость абсолютного нуля температуры. Если предположить, что абсолютный нуль достижим, тогда можно в качестве холодильника обратимого цикла Карно взять тело с температурой T 2 = 0. По теореме Нернста изотерма T = 0 одновременно является адиабатой. Следовательно, энтропия нагревателя также не изменяется, т. е. рабочее тело не получает от нагревателя теплоту. Противоречие доказывает недостижимость абсолютного нуля. 2. Теплоемкость, коэффициент теплового расширения и некоторые другие аналогичные величины должны стремиться к нулю при температуре, стремящейся к нулю.
cx = T (¶ S / ¶ T) x = (¶ S / ¶ ln T) x → 0,
α p = V –1 (¶ V / ¶ T) p = – V –1 (¶ S / ¶ p) T → 0 при T → 0.
Данное следствие доказывает, что теплоемкость вещества обязательно должна зависеть от температуры. Классическая теория теплоемкости приводит к противоположному результату. Поэтому теорема Нернста не может быть истолкована с классических позиций. 3. Модель идеального газа не применима при очень низких температурах (при T → 0). Теореме Нернста противоречит хотя бы то, что для идеального газа α p → ∞ при T → 0.
|

 S (T, x) = S 0. (50.1)
S (T, x) = S 0. (50.1)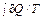 сходится.
сходится.


