Термодинамические потенциалы сложных систем
Термодинамические потенциалы H, F, G были введены для такой простой системы, как газ. Однако все сказанное несложно обобщить на другие физические системы, в том числе на системы со многими степенями свободы. Для этого надо в качестве элементарной работы взять соответствующее выражение и подставить его в основное уравнение термодинамики (29.8). Для закрытых систем со многими степенями свободы уравнение примет вид
dU = TdS –
где xi – обобщенные координаты, а Xi – обобщенные силы. Если состояние системы определяется внешними параметрами xi и энтропией, то термодинамическим потенциалом является внутренняя энергия U (S, x 1, x 2, …), дифференциал которой выписан выше (см. (44.1)). Энтальпия, по определению, равна
H = U + Ее естественные переменные – энтропия и обобщенные силы, а дифференциал равен
dH = TdS +
Если независимыми переменными являются внешние параметры xi и температура, то состояние системы полностью описывается свободной энергией
F = U – T × S.
Ее дифференциал
dF = – SdT –
Наконец, для переменных: температура и обобщенные силы – термодинамическим потенциалом является функция
G = F + с дифференциалом
dG = – SdT +
Помимо этих потенциалов существует большое число других подобных функций, которые могут быть построены последовательным применением преобразования Лежандра по переменным x 1, x 2, …, X 1, X 2, …. В случае открытой системы число частиц является переменным. Изменение числа частиц может происходить в результате фазовых переходов, химических реакций и т. д. Основное уравнение термодинамики (29.8) для открытых систем содержит соответствующее слагаемое
dU = TdS – pdV +
Определения всех других термодинамических потенциалов сохраняются, т. е.
H = U + pV, F = U – TS, G = H – TS.
Их дифференциалы равны
dH = TdS + Vdp +
dG = – SdT + Vdp +
Для химического потенциала из этих выражений следуют равенства
μ i =
Термодинамические потенциалы – экстенсивные величины. В случае системы из одинаковых частиц это означает, что при изменении массы вещества или числа частиц N в некоторое число раз, во столько же раз изменятся и значения термодинамических потенциалов. Следовательно, зависимость термодинамических потенциалов от числа частиц должна быть такой:
U = N × f 1(S / N, V / N), H = N × f 2(S / N, p), F = N × f 3(T, V / N), G = N × f 4(T, p).
Отсюда получается, что μ = f 4(T, p), т. е. химический потенциал равен потенциалу Гиббса в расчете на одну частицу, и, значит,
G = N × μ. (44.4)
Для других потенциалов подобного равенства не существует. Например:
μ = (¶ F / ¶ N) T,V ≠ f 3(T, V / N) = F / N.
Соотношение (44.4) обобщается на любую смесь веществ. Потенциал Гиббса смеси равен
G =
В самом деле, при изменении полного числа частиц в α раз изменяются в α раз и число частиц каждого сорта и потенциал Гиббса, т. е.
G (T, p, α N 1, α N 2, …) = α
Дифференцирование этого равенства по α дает
Если положить α = 1, то получится уравнение Эйлера
Замена производных на химические потенциалы приводит к равенству (44.5). Исключение потенциала G из соотношений (44.3), (44.5) позволяет получить важное в термодинамике уравнение Гиббса–Дюгема
SdT – Vdp +
|

 , (44.1)
, (44.1)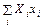 .
. .
.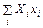
 . (44.2)
. (44.2)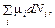
 (44.3)
(44.3)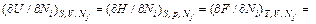
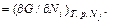
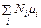 . (44.5)
. (44.5)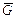 (T, p, N 1, N 2, …).
(T, p, N 1, N 2, …).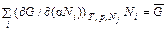 .
.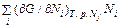 = G.
= G.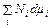 = 0. (44.6)
= 0. (44.6)


