Термодинамика газа Ван-дер-Ваальса
Ниже аппарат термодинамики применяется для изучения свойств газа Ван-дер-Ваальса. Его термическое уравнение состояния имеет вид
p = ν RT / (V – ν b) – a ν2 / V 2, (48.1)
где a и b – постоянные, различные для разных газов, ν – число молей. Эта модель приближенно описывает жидкое и газообразное состояния вещества и переход из одного состояния в другое.
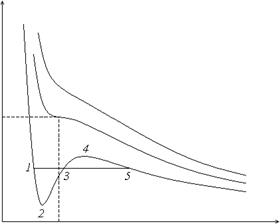
На (p, V)-диаграмме (рис. 18) изотермы газа Ван-дер-Ваальса имеют при низких температурах максимум и минимум. Левая круто падающая ветвь отвечает жидкому состоянию (некоторое изменение объема при большом перепаде давления говорит о малой сжимаемости вещества), правая пологая ветвь – газообразному состоянию. На участке 2–3–4 кривой состояние абсолютно неустойчиво и не реализуется. Переход из жидкого состояния в газообразное состояние и наоборот происходит на самом деле по изотерме-изобаре 1–3–5 через последовательность двухфазных состояний; при этом ближе к точке 1 больше жидкости, а ближе к точке 5 – насыщенного пара. Существует правило Максвелла, согласно которому площади, образующиеся при пересечении изотермы-изобары с изотермой Ван-дер-Ваальса, равны. Доказать это просто, если рассмотреть равновесный круговой процесс 1–2–3–4–5–3–1 и воспользоваться основным уравнением термодинамики:
Работа за цикл равна нулю. Ее можно разбить на два слагаемых: положительную работу A 3453 и отрицательную A 1231. Они равны по величине, что и означает равенство площадей. Участок 1–2 изотермы Ван-дер-Ваальса соответствует переохлажденной жидкости, а 4–5 – пересыщенному пару. Это метастабильные состояния. При повышении температуры все перечисленные точки сближаются. При некоторой температуре Tк, называемой критической, они сливаются. Это критическая точка. В ней
(¶ p /¶ V) T = 0 и (¶2 p /¶ V 2) T = 0, (48.2)
т. е. изотерма Ван-дер-Ваальса в этой точке имеет нулевой наклон, а сама точка является точкой перегиба. После вычисления производных уравнения (48.2) принимают вид
– ν RT /(V – ν b)2 + 2 a ν2/ V 3 = 0 и 2ν RT /(V – ν b)3 – 6 a ν2/ V 4 = 0. (48.3)
Решение системы уравнений (48.1), (48.3) дает критические параметры
Vк = 3ν b, Tк = 8 a /(27 Rb), pк = a /(27 b 2). (48.4)
При температурах T > Tк состояние вещества всюду газообразное, притом чем выше температура, тем изотермы ближе к изотермам идеального газа pV = const. Из соотношения (42.2) следует, что теплоемкость cV газа Ван-дер-Ваальса не зависит от объема:
(¶ cV /¶ V) T = T (¶2 p /¶ T 2) V = 0. Если считать зависимость ее от температуры известной, можно найти внутреннюю энергию и энтропию газа Ван-дер-Ваальса. В переменных T, V
dU = (¶ U /¶ T) VdT + (¶ U /¶ V) TdV = ν cV dT + (T (¶ p /¶ T) V – p) dV
(здесь использованы полученные раньше соотношения (15.3), (26.1)), или с учетом термического уравнения состояния (48.1)
dU = ν cV (T) dT + a ν2/ V 2 dV.
После интегрирования получается
U = ν(
Внутренняя энергия пропорциональна числу молей (выражение в скобках представляет внутреннюю энергию одного моля, она определяется температурой и молярным объемом V /ν). При расширении газа Ван-дер-Ваальса в пустоту его температура согласно (48.5) уменьшается. Если использовать основное уравнение термодинамики
TdS = dU + pdV = ν cV dT + ν RT /(V – ν b) dV,
то
dS = ν cV dT / T + ν R /(V – ν b) dV,
откуда
S = ν(
или
S = ν(
т. е. энтропия также пропорциональна числу молей. Можно вычислить и другие термодинамические характеристики газа Ван-дер-Ваальса.
49. Теория процесса Джоуля–Томсона
Для иллюстрации эффективности применения термодинамического аппарата в исследованиях физических систем рассматривается процесс Джоуля–Томсона. Экспериментальные исследования, выполненные совместно Джоулем и В. Томсоном в 1852–1862 гг., позволили ответить на вопрос о зависимости внутренней энергии газа от объема. Более того, в результате этих исследований было открыто важное физическое явление, получившее название эффекта Джоуля–Томсона.
В опытах Джоуля и Томсона бралась цилиндрическая трубка, окруженная теплоизолирующим материалом (рис. 19). В середине трубки между двумя металлическими сетками помещалась пробка из плотной ваты или очесов шелка. Исследуемый газ под действием разности давлений (p 1 > p2) протекал через пробку. Пробка обеспечивала спокойное, медленное перетекание газа. Его кинетической энергией можно было пренебречь. Газ по обе стороны пробки в любой момент времени находился в равновесных состояниях. Между собой газ и пробка во время процесса обменивались теплотой. Однако, когда процесс становился стационарным, теплообмен прекращался и физическое состояние пробки не менялось, ее внутренняя энергия оставалась неизменной, устанавливались постоянные температуры газа T 1 и T 2 перед и за пробкой соответственно. Эти температуры и измерялись. Стационарное течение газа через пробку называется процессом Джоуля–Томсона, а изменение температуры при таком течении называют эффектом Джоуля–Томсона. Процесс и эффект Джоуля–Томсона могут наблюдаться в производственных условиях: при течении в трубе через вентиль (перепад давления создается, например, компрессором). Несложно показать, что в процессе Джоуля–Томсона энтальпия газа сохраняется. Пусть газ, занимавший вначале объем V 1 слева от пробки, после продавливания имеет объем V 2. В стационарном режиме подвод теплоты к газу отсутствует. Поэтому изменение его внутренней энергии равно работе, производимой над ним:
U 2 – U 1 = p 1 V 1 – p 2 V 2,
откуда следует, что
H 2 = H 1.
Рассматриваемый процесс является неравновесным: в результате его осуществления энтропия газа (несмотря на отсутствие подвода теплоты) возрастает. Это легко показать. Реальный процесс мысленно заменяется равновесным, ведущим к тому же конечному состоянию. Для равновесного процесса справедливо основное уравнение. Если взять его в виде выражения (38.4) для дифференциала энтальпии, то при H = const из него следует, что
(¶ S /¶ p) H = – V / T < 0.
Поскольку давление газа падает, то энтропия в воображаемом равновесном процессе (и, стало быть, в реальном также) возрастает. Интерес представляет изменение температуры газа. Оно будет, очевидно, таким же, как в воображаемом изоэнтальпическом процессе, т. е.
Δ T = и характеризуется производной (¶ T /¶ p) H. Пусть при ее вычислении известными считаются термическое уравнение состояния газа и его теплоемкость при постоянном давлении. Тогда, сделав переход к якобианам, использовав естественные переменные для энтальпии, а также воспользовавшись соотношением взаимности (38.5) и формулой (38.7) для cp, можно найти искомую производную:
(¶ T /¶ p) H = ¶(T, H) / ¶(p, H) = ¶(T, H) / ¶(S, p) × ¶(S, p) / ¶(p, H) =
= – (¶ T / ¶ S) p (¶ H / ¶ p) S (¶ S / ¶ H) p + (¶ T / ¶ p) S = – V / cp + (¶ V / ¶ S) p =
= – V / cp + (¶ V / ¶ T) p (¶ T / ¶ S) p = cp –1(T (¶ V / ¶ T) p – V) =
= – cp –1(T (¶ V / ¶ p) T (¶ p / ¶ T) V + V).
Окончательно
(¶ T / ¶ p) H = – λ cp –1(¶ V / ¶ p) T, (49.1)
где λ = T (¶ p / ¶ T) V + V (¶ p / ¶ V) T. При выводе формулы (49.1) применялись соотношения (43.4) и (43.5). Из формулы (49.1) следует, что в случае идеального газа эффект Джоуля–Томсона отсутствует, т. е. (¶ T / ¶ p) H = 0. Для реальных газов знак (¶ T / ¶ p) H совпадает со знаком λ ((¶ V / ¶ p) T < 0). При λ < 0 эффект Джоуля–Томсона отрицательный (газ при продавливании сквозь пробку нагревается); при λ > 0 эффект положительный (газ охлаждается). В точке инверсии (λ = 0) происходит смена знака эффекта. В случае газа Ван-дер-Ваальса (p = RT / (V – b) – a / V 2 для одного моля, (¶ p / ¶ T) V = R / (V – b), (¶ p / ¶ V) T = – RT / (V – b)2 + 2 a / V 3)
λ = – RTb / (V – b)2 + 2 a / V 2. (49.2)
Пусть в формуле (49.2) λ = 0. Тогда 1 – b / V =
p = 2 a / b 2 × x (1 – x) – a / b 2 × (1 – x)2,
или x 2 – 4 x / 3 + (1 + b 2 p / a) / 3 = 0.
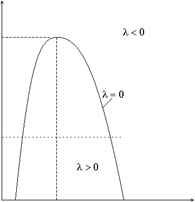
При заданном давлении получилось квадратное уравнение относительно корня из температуры инверсии. Соответствующая кривая инверсии имеет куполообразную форму в плоскости p, T (рис. 20, pк, Tк – критические давление и температура). Область положителного эффекта лежит внутри кривой (это видно хотя бы из того, что при T → ∞ и фиксированном объеме параметр λ становится отрицательным). При p < 9 pк существуют две точки инверсии. Для большинства газов нижняя точка инверсии находится в области жидких состояний, а верхние температуры инверсии велики по сравнению с комнатными. С этим связано техническое использование процесса Джоуля–Томсона для сжижения таких газов, как азот, кислород и т. д. Для водорода и гелия верхние температуры инверсии при обычно употребляемых давлениях значительно ниже комнатной температуры, и необходимо предварительное охлаждение этих газов (см. таблицу, в которой приведены значения критических параметров некоторых газов).
Из выражения (49.2) для λ газа Ван-дер-Ваальса видно, что положительный эффект Джоуля–Томсона наблюдается, когда большую роль играет поправка a / V 2, а отрицательный – когда преобладает поправка b. Первая поправка связана с силами притяжения между молекулами. Эти силы препятствуют ускорению молекул при расширении газа в результате прохождения пробки, уменьшая кинетическую энергию молекул и, следовательно, температуру газа. Поправка b связана с конечными размерами молекул, т. е. с силами отталкивания. Они, наоборот, ускоряют молекулы: кинетическая энергия молекул и температура газа возрастают. Интересно сравнить падение температуры в процессе Джоуля–Томсона с ее падением при адиабатическом расширении (перепад давления один и тот же). Для этого вычисляется коэффициент
(¶ T / ¶ p) S = ¶(T, S) / ¶(p, S) = ¶(p, V) / ¶(p, S) = ¶(p, V) / ¶(p, T) × ¶(p, T) / ¶(p, S) =
= T / cp × (¶ V / ¶ T) p.
В результате
(¶ T / ¶ p) S = T / cp × (¶ V / ¶ T) p > 0. (49.3)
Для процесса Джоуля–Томсона было получено
(¶ T / ¶ p) H = T / cp × ((¶ V / ¶ T) p – V / T).
Видно, что (¶ T / ¶ p) H < (¶ T / ¶ p) S. Таким образом, падение температуры при адиабатическом расширении является более сильным.
|

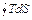 = T
= T  = 0 =
= 0 = 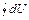 +
+ 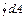 =
= 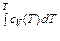 – a ν/ V + const). (48.5)
– a ν/ V + const). (48.5)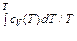 + R ×ln (V – ν b) + const (ν)),
+ R ×ln (V – ν b) + const (ν)),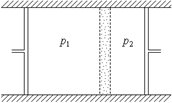 Рис. 19
Рис. 19
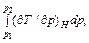
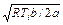 = x (Ti – температура инверсии). Отсюда V = b / (1 – x), V – b = bx / (1 – x). Исключение V из уравнения Ван-дер-Ваальса дает
= x (Ti – температура инверсии). Отсюда V = b / (1 – x), V – b = bx / (1 – x). Исключение V из уравнения Ван-дер-Ваальса дает


