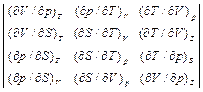Термодинамические коэффициенты

 

В теории термодинамических потенциалов приходится иметь дело с различными производными. Термодинамическими коэффициентами называют выражения вида (¶λ / ¶μ)_ν, где совокупность λ, μ, ν – комбинация трех величин из p, V, T, S. Можно составить 12 различных термодинамических коэффициентов. Они характеризуют определенные свойства системы. Так, коэффициенты объемного расширения (изобарический и адиабатический) α _p и α _S определяются по формулам

 

α _p = V ^–1(¶ V / ¶ T) _p, α _S = V ^–1(¶ V / ¶ T) _S; (43.1)

 

термические коэффициенты давления (изохорический и адиабатический) β _V и β _S равны

β _V = p ^–1(¶ p / ¶ T) _V, β _S = p ^–1(¶ p / ¶ T) _S. (43.2)

 

Аналогичные формулы имеются для вычисления изотермической и адиабатической сжимаемостей γ _T и γ _S:

 

γ _T = – V ^–1(¶ V / ¶ p) _T, γ _S = – V ^–1(¶ V / ¶ p) _S. (43.3)

 

Наконец, изохорическая и изобарическая теплоемкости c_V и c_p вычисляются по соотношениям

 

c_V = T (¶ S / ¶ T) _V, c_p = T (¶ S / ¶ T) _p.

 

Из 12 термодинамических коэффициентов независимыми являются три. Это можно показать с помощью составленной из коэффициентов таблицы:

 

 

Первая строка таблицы не содержит S, вторая – p, третья – V и последняя (четвертая) не содержит T. Произведение коэффициентов в одной строке равно –1. Получаются четыре соотношения:

 

(¶λ / ¶μ)_ν × (¶μ / ¶ν)_λ × (¶ν / ¶λ)_μ = –1. (43.4)

 

Производные при одной и той же постоянной величине дают еще четыре соотношения:

 

(¶λ / ¶μ)_δ × (¶μ / ¶ν)_δ = (¶λ / ¶ν)_δ, (43.5)

 

где λ, μ, ν, δ – комбинация из p, V, T, S.

Девятым является соотношение (35.4):

 

¶(T, S) / ¶(p, V) = 1.

 

Таким образом, имеются девять уравнений (35.4), (43.4) и (43.5) для 12 термодинамических коэффициентов. В качестве трех независимых коэффициентов целесообразно выбрать

 

(¶ V / ¶ p) _T = – γ _T × V, (¶ p / ¶ T) _V = β _V × p, (¶ S / ¶ T) _V = c_V / T. (43.6)

 

Они сравнительно легко могут быть найдены из эксперимента либо несложным образом вычисляются: первые два – по известному термическому уравнению состояния, а c_V – методами статистической физики (зависимость c_V от объема определяется, если известно термическое уравнение состояния; см. формулу (42.2)).