Термодинамический потенциал Гиббса
Наконец, температура и давление являются естественными независимыми переменными для термодинамического потенциала Гиббса:
G = G (T, p) = U – TS + pV = H – TS = F + pV. (40.1)
Если следовать преобразованию Лежандра, то x = S, y = V, X = T, y = – p, L = U и
dG = – SdT + Vdp. (40.2)
Сам потенциал и его дифференциал можно получить также, преобразуя непосредственно основное уравнение термодинамики (29.9):
dU = TdS – pdV = d (TS) – SdT – d (pV) + Vdp, откуда
d (U – TS + pV) = dG = – SdT + Vdp.
Легко найти условие того, что выражение (40.2) для dG является полным дифференциалом:
– (¶ S / ¶ p) T = – ¶(T, S) / ¶(T, p) = – ¶(p, V) / ¶(T, p) = ¶(V, p) / ¶(T, p) = (¶ V / ¶ T) p,
т. е. соотношение взаимности в данном случае имеет вид
– (¶ S / ¶ p) T = (¶ V / ¶ T) p. (40.3)
Термические свойства определяются дифференцированием потенциала по давлению:
V = (¶ G / ¶ p) T = V (T, p),
а энтропия – дифференцированием по температуре:
S = – (¶ G / ¶ T) p. = S (T, p). (40.4)
Вторые производные от G (T, p) дают теплоемкость cp и изотермический коэффициент сжимаемости γ:
cp = T (¶ S / ¶ T) p = – T (¶2 G / ¶ T 2) p,
γ = – V –1(¶ V / ¶ p) T = – (¶2 G / ¶ p 2) T / (¶ G / ¶ p) T.
Термодинамический потенциал Гиббса и энтальпия связаны друг с другом дифференциальным уравнением (уравнением Гиббса–Гельмгольца), получаемым из соотношений (40.1) и (40.4):
H = G – T (¶ G / ¶ T) p. (40.5)
Если известна какая-либо информация об одном из этих потенциалов (H или G), то уравнение позволяет получить какие-то сведения и о другом потенциале. Если на систему помимо сил давления действуют еще немеханические силы, то основное уравнение термодинамики принимает вид
dU = TdS – pdV – δ Aнм.
Последнее слагаемое в правой части представляет работу системы, связанную с немеханическими силами. Дифференциал термодинамического потенциала с учетом этой работы равен
dG = – SdT + Vdp – δ Aнм,
откуда видно, что при изотермически-изобарических процессах система совершает работу против немеханических сил, которая равна убыли термодинамического потенциала:
δ Aнм = – (dG) T,p.
Таким образом, в переменных T и p термодинамическим потенциалом является потенциал Гиббса.
|

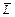 = U – TS + pV = G. Тогда полный дифференциал потенциала Гиббса равен
= U – TS + pV = G. Тогда полный дифференциал потенциала Гиббса равен


