Якобианы. Свойства
IV. Теория термодинамических потенциалов
Якобианы. Свойства
Пусть в области Ω на плоскости x, y задана функция f (x, y) и требуется вычислить интеграл
I =
В частном случае, когда подынтегральная функция равна единице, этот интеграл дает площадь области Ω. При вычислении интеграла иногда лучше перейти к другим независимым переменным. Пусть это будут ξ и η. Старые и новые независимые переменные связаны некоторыми функциональными уравнениями
x = x (ξ, η), y = y (ξ, η). (34.1)
При этом область Ω на плоскости x, y преобразуется в область ω на плоскости ξ, η. При переходе к новым переменным интеграл примет вид
I =
Здесь D – функциональный определитель (якобиан) для двух переменных:
D = ¶(x, y) / ¶(ξ, η) = (34.2) = (¶ x / ¶ξ)(¶ y / ¶η) – (¶ x / ¶η)(¶ y / ¶ξ).
Геометрический смысл его заключается в том, что абсолютная величина D дает коэффициент изменения элементарной площади при переходе от (x, y)- к (ξ, η)-плоскости. Поведение якобиана преобразования (x, y) ® (ξ, η) имеет непосредственное отношение к вопросу об однозначности соответствия между точками (x, y)- и (ξ, η)-плоскостей. Пусть достаточно малой окрестности точки (ξ, η) согласно уравнениям (34.1) отвечает множество точек (x, y). Доказывается теорема. Если функции (34.1) непрерывно дифференцируемы в некоторой области значений переменных ξ, η и если якобиан (34.2) отличен в ней от нуля, то в достаточно малой окрестности произвольной точки (ξ, η) этой области уравнения (34.1) определяют взаимно однозначное соответствие этой окрестности точки (ξ, η) и отвечающего ей множества точек (x, y). Другими словами, каждой точке первой области соответствует одна и только одна точка второй области, и наоборот. Теорема является простым следствием известной теоремы Крамера из алгебры линейных уравнений. Между дифференциалами величин x, y, ξ, η имеются линейные связи
dx = (¶ x /¶ξ) d ξ + (¶ x /¶η) d η,
dy = (¶ y /¶ξ) d ξ + (¶ y /¶η) d η.
Для того чтобы эта система уравнений была разрешима относительно d ξ и d η, и чтобы решение ее было единственным, определитель из коэффициентов (как раз якобиан D) должен быть отличен от нуля. В противном случае решение или отсутствует, или неоднозначно. Якобиан (34.2) тождественно равен нулю, если функции (34.1) не являются независимыми, т. е. между ними существует функциональная связь. Указанная теорема имеет особое значение в термодинамике в связи с широким использованием геометрических образов на (p, V) –, (T, S) – и других диаграммах. В дальнейшем будут использоваться следующие свойства якобианов: 1. При перестановке функций или независимых переменных изменяется знак якобиана:
¶(x, y)/¶(ξ, η) = – ¶(y, x)/¶(ξ, η) = ¶(y, x)/¶(η, ξ).
2. Теорема умножения якобианов.
¶(x, y)/¶(u, v) = ¶(x, y)/¶(ξ, η) × ¶(ξ, η)/¶(u, v).
Она следует из известных формул дифференциального исчисления вида
(¶ x /¶ u) v = (¶ x /¶ξ)η × (¶ξ/¶ u) v + (¶ x /¶η)ξ × (¶η/¶ u) v.
Это формулы дифференцирования сложных функций, когда x и y зависят от u и v не прямо, а через посредство функций ξ(u, v) и η(u, v). Действительно, пусть
x = x (ξ(u, v), η(u, v)), y = y (ξ(u, v), η(u, v)).
Тогда
¶(x, y)/¶(u, v) = (¶ x /¶ u) v (¶ y /¶ v) u – (¶ x /¶ v) u (¶ y /¶ u) v =
= ¶ x /¶ξ × ¶ y /¶ξ × (¶ξ/¶ u × ¶ξ/¶ v – ¶ξ/¶ v × ¶ξ/¶ u) +
+ ¶ x /¶ξ × ¶ y /¶η × (¶ξ/¶ u × ¶η/¶ v – ¶ξ/¶ v × ¶η/¶ u) +
+ ¶ x /¶η × ¶ y /¶ξ × (¶η/¶ u × ¶ξ/¶ v – ¶η/¶ v × ¶ξ/¶ u) +
+ ¶ x /¶η × ¶ y /¶η × (¶η/¶ u × ¶η/¶ v – ¶η/¶ v × ¶η/¶ u) =
= (¶ x /¶ξ × ¶ y /¶η – ¶ x /¶η × ¶ y /¶ξ) × (¶ξ/¶ u × ¶η/¶ v – ¶ξ/¶ v × ¶η/¶ u) =
= ¶(x, y)/¶(ξ, η) × ¶(ξ, η)/¶(u, v).
Свойство доказано. 3. Если использовать предыдущее свойство и положить u = x и v = y, то получается выражение для обратного якобиана:
¶(ξ, η)/¶(x, y) = (¶(x, y)/¶(ξ, η))–1.
4. Частную производную можно записать в виде якобиана. Пусть y ≡ η. Тогда (¶ y /¶ξ)η = 0 и (¶ y /¶η)ξ = 1. Поэтому
¶(x, η)/¶(ξ, η) =
Итак,
35. Якобиан преобразования (T, S) →(p, V)
Внутренняя энергия U – функция состояния. Если начальное и конечное состояния совпадают, то изменение внутренней энергии в процессе равно нулю независимо от промежуточных состояний системы (для них внутренняя энергия может и не определяться). Таким образом, для произвольного кругового процесса
Δ U = 0. (35.1)
Если круговой процесс равновесный, то вместо равенства (35.1) можно написать
В силу равенства (35.2) из основного термодинамического тождества (29.9) для закрытых систем следует
Справа в этом интегральном соотношении работа A системы за круговой процесс; она равна площади этого процесса на (p, V)-диаграмме. Слева количество теплоты Q, полученное системой за тот же круговой процесс. Данный процесс можно рассмотреть также и на (T, S)-диаграмме. Площадь на ней за круговой процесс численно равна Q. Соотношение (35.3) выражает эквивалентность площадей на (p, V)- и (T, S)-диаграммах (равенство работы A и теплоты Q). К слову сказать, (T, S)-диаграмма часто используется в термодинамических исследованиях. На ней обратимый цикл Карно представляется в виде прямоугольника (рис. 15).
Из равенства площадей на (p, V)- и (T, S)-диаграммах следует, что якобиан преобразования (T, S) ® (p, V) равен единице:
¶(T, S)/¶(p, V) = 1. (35.4)
Это калибровочное соотношение. Оно устанавливает соответствие между температурной и энтропийной шкалами. Шкала для измерения геометрических величин: длины, площади, объема – и шкала для силы, в том числе давления, установлены в механике; выше введена температурная шкала. Соотношение (35.4) определяет шкалу энтропии, или, в более широком смысле, устанавливает соответствие между шкалами T и S. Одновременно соотношение (35.4) есть условие того, что правая часть тождества (29.9) – полный дифференциал. В самом деле, если внутренняя энергия задана как функция энтропии и объема
U = U (S, V), (35.5)
то ее первый (полный) дифференциал равен
dU = (¶ U /¶ S) VdS + (¶ U /¶ V) SdV.
Сравнение его с выражением (29.9) дает
(¶ U /¶ S) V = T, (¶ U /¶ V) S = – p. (35.6)
Повторным дифференцированием можно получить
¶2 U / (¶ V ¶ S) = (¶ T /¶ V) S, ¶2 U / (¶ S ¶ V) = – (¶ p /¶ S) V.
Отсюда на основании известной из математического анализа теоремы о перемене порядка дифференцирования следует соотношение взаимности, или соотношение Максвелла
(¶ T /¶ V) S = – (¶ p /¶ S) V. (35.7)
Оно является условием того, что выражение (29.9) для dU – полный дифференциал. Если теперь перейти в этом условии к якобианам, поделив предварительно на правую часть, то оно примет вид условия калибровки (35.4).
|

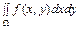 .
. .
. =
= =
=  .
.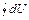 = 0. (35.2)
= 0. (35.2) , или
, или  . (35.3)
. (35.3)



