Метод термодинамических потенциалов. Примеры применения
Метод исследования термодинамических систем с помощью термодинамических потенциалов является очень удобным и в настоящее время наиболее употребительным. В основе этого метода, называемого методом термодинамических потенциалов, лежит применение соотношений взаимности (35.7), (38.5), (39.4), (40.3). Они используются для получения различных соотношений между величинами, характеризующими равновесные состояния системы. Ниже приведен ряд примеров такого использования. Пример 1. Известно термическое уравнение состояния p = p (T, V). Необходимо найти производную (¶ U / ¶ V) T. Решение. Основное уравнение (29.9) делится на dV, при этом температура полагается постоянной:
(¶ U / ¶ V) T = T (¶ S / ¶ V) T – p.
Применение соотношения (39.4) приводит к ответу:
(¶ U / ¶ V) T = T (¶ p / ¶ T) V – p.
Это уравнение уже было получено раньше методом циклов. Если известны термические свойства системы, уравнение позволяет найти зависимость внутренней энергии от объема. Пример 2. При заданном термическом уравнении состояния найти производную (¶ H / ¶ p) T. Решение. Рассматривается изотермический процесс. Для него записывается уравнение (38.4). После деления этого уравнения на dp и использования соотношения (40.3) получается искомое выражение для производной:
(¶ H / ¶ p) T = T (¶ S / ¶ p) T + V = – T (¶ V / ¶ T) p + V,
т. е.
(¶ H / ¶ p) T = – T (¶ V / ¶ T) p + V. (42.1) Пример 3. Для известного термического уравнения состояния найти производную (¶ cV / ¶ V) T. Решение. По определению cV = (δ Q / ¶ T) V, или так как δ Q = TdS, то cV = T (¶ S / ¶ T) V. Дифференцирование cV по объему при постоянной температуре дает (¶ cV / ¶ V) T = T ¶ 2 S / (¶ V ¶ T). Изменение порядка дифференцирования и использование соотношения (39.4) позволяет найти искомую производную:
(¶ cV / ¶ V) T = T ¶(¶ S / ¶V) T / ¶ T = T (¶2 p / ¶ T 2) V.
Таким образом,
(¶ cV / ¶ V) T = T (¶2 p / ¶ T 2) V, (42.2)
и если известно термическое уравнение состояния, то может быть установлена зависимость теплоемкости cV от объема. Аналогично можно получить формулу
(¶ cp / ¶ p) T = – T (¶2 V / ¶ T 2) p. (42.3)
Пример 4. Термическое уравнение состояния задано в виде p = p (T, V). Найти разность теплоемкостей cp и cV. Решение. Теплоемкость системы связана с производной от энтропии: C = T (¶ S / ¶ T). В частности,
cp = T (¶ S / ¶ T) p, cV = T (¶ S / ¶ T) V.
Чтобы перейти от cp к cV, надо в выражении для cp вместо независимых переменных T, p ввести переменные T, V. При такой замене
(¶ S / ¶ T) p = (¶ S / ¶ T) V + (¶ S / ¶ V) T × (¶ V / ¶ T) p,
так что
cp = cV + T (¶ S / ¶ V) T × (¶ V / ¶ T) p.
Производная (¶ V / ¶ T) p вычисляется с помощью якобианов:
(¶ V / ¶ T) p =
Используется еще соотношение Максвелла (39.4). В результате искомая разность теплоемкостей равна
cp – cV = – T
Для устойчивости термодинамического равновесия необходимо, чтобы производная (¶ p / ¶ V) T была отрицательной. Это приводит к неравенству
cp ≥ cV. (42.5)
Пример 5. Показать, что на (p, V)-диаграмме адиабаты с ростом V падают круче изотерм. Учесть, что cp ≥ cV > 0 и (¶ p / ¶ V) T < 0. Решение. Наклон адиабат и изотерм определяется соответственно производными (¶ p / ¶ V) S и (¶ p / ¶ V) T. Следовательно, для решения задачи необходимо рассмотреть производную (¶ p / ¶ V) S и перейти от переменных S, V к переменным T, V. Наиболее быстро результат может быть получен, если частные производные заменить на соответствующие якобианы и учесть, что теплоемкость c = T (¶ S / ¶ T). Тогда
(¶ p / ¶ V) S = ¶(S, p) / ¶(S, V) = ¶(S, p) / ¶(T, p) × ¶(T, p) / ¶(T, V) × ¶(T, V) / ¶(S, V) =
= (¶ S / ¶ T) p × (¶ p / ¶ V) T / (¶ S / ¶ T) V = cp / cV × (¶ p / ¶ V) T.
Итак,
(¶ p / ¶ V) S = cp / cV × (¶ p / ¶ V) T. (42.6)
Отсюда следует, что
(¶ p / ¶ V) S < (¶ p / ¶ V) T.
Пример 6. Установить, как изменяется температура в процессе Гей-Люссака. Термическое уравнение состояния известно. Решение. Необходимо напомнить, что представляет собой процесс Гей-Люссака. Газ из сосуда, если открыть кран, устремляется в другой сосуд, который перед тем был откачан. Равновесие в системе устанавливается достаточно быстро, и теплообмен через стенки сосудов можно не учитывать: Q = 0. Работа также не совершается: A = 0 (сосуды имеют жесткие стенки). Следовательно, внутренняя энергия газа в результате неравновесного расширения не изменяется. Поскольку температура – функция состояния, то ее изменение в данном процессе будет таким же, как в равновесном процессе при постоянной внутренней энергии. Таким образом,
Δ T =
где V 1, V 2 – объемы сосудов с газом и без него. Задача свелась к вычислению производной (¶ T / ¶ V) U. Для ее вычисления делается переход к якобианам, используются естественные переменные для внутренней энергии: энтропия и объем. Следует заметить, что всякий раз, как рассматриваются производные, связанные с тем или иным термодинамическим потенциалом, целесообразно при использовании аппарата якобианов переходить к переменным, естественным для данного потенциала. Итак,
(¶ T / ¶ V) U = ¶(T, U) / ¶(V, U) = (¶(T, U) / ¶(S, V)) / (¶(V, U) / ¶(S, V)) =
= ((¶ T / ¶ S) V × (¶ U / ¶ V) S – (¶ T / ¶ V) S × (¶ U / ¶ S) V) / (– (¶ U / ¶ S) V) =
= – (¶ T / ¶ S) V × (¶ U / ¶ V) S / (¶ U / ¶ S) V + (¶ T / ¶ V) S.
Из выражения для дифференциала внутренней энергии следует (см. соотношения (35.6))
(¶ U / ¶ S) V = T, (¶ U / ¶ V) S = – p.
Возможность использования этих соотношений является причиной перехода к естественным переменным. Кроме того, из соотношения (35.7)
(¶ T / ¶ V) S = – (¶ p / ¶ S) V = – ¶(p, V) / ¶(S, V) =
= – ¶(p, V) / ¶(T, V) × ¶(T, V) / ¶(S, V)= – (¶ p / ¶ T) V × (¶ T / ¶ S) V, так что
(¶ T / ¶ V) U = (¶ T / ¶ S) V × (p / T – (¶ p / ¶ T) V).
Теплоемкость cV связана с энтропией S соотношением (37.2): cV = T (¶ S / ¶ T) V, откуда (¶ T / ¶ S) V = T / cV. Окончательно
(¶ T / ¶ V) U =
Для идеального газа (¶ T / ¶ V) U = 0. В опытах Гей-Люссака в пределах погрешности оказалось, что T 2 = T 1. Из этого факта следует вывод о независимости внутренней энергии газа от объема. Для газа Ван-дер-Ваальса
p = RT / (V – b) – a / V 2 и (¶ p / ¶ T) V = R / (V – b),
так что
(¶ T / ¶ V) U = – a / (V 2 cV) < 0,
т. е. для реальных газов процесс Гей-Люссака должен сопровождаться небольшим охлаждением. В опытах Гей-Люссака, из-за низкой теплоемкости газа по сравнению с теплоемкостью стенок сосудов, погрешность большая, поэтому охлаждение газа не было замечено.
|
= – (¶ p / ¶ T) V / (¶ p / ¶ V) T.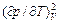
/ (¶ p / ¶ V) T. (42.4)
,
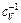(p – T (¶ p / ¶ T) V).
