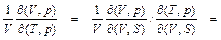Внутренняя энергия как термодинамический потенциал

 

К числу термодинамических потенциалов относится внутренняя энергия, заданная как функция энтропии и объема (35.5). Параметры S и V являются естественными переменными для U. Дифференциал внутренней энергии определяется основным уравнением (29.9), и он полный. Это дает соотношение взаимности (35.7), называемое также соотношением Максвелла. Простое дифференцирование U (S, V) по S и V позволяет получить систему двух уравнений (см. соотношения (35.6))

 

T = (¶ U /¶ S) _V = T (S, V), p = – (¶ U / ¶ V) _S = p (S, V), (37.1)

 

которую можно рассматривать как параметрическое задание термического уравнения состояния. Если из первого уравнения этой системы выразить энтропию через температуру и объем и подставить во второе уравнение, то термическое уравнение состояния примет обычный вид p = p (T, V). Исключая S из выражения (35.5) для U, можно получить калорическое уравнение состояния U = U (T, V). С помощью операции дифференцирования и арифметических операций могут быть найдены все термодинамические величины, характеризующие физическую систему. Пусть, к примеру, требуется найти теплоемкость при постоянном объеме. Так как для равновесных процессов δ Q = TdS, то теплоемкость системы связана с энтропией соотношением c _x = T (¶ S /¶ T)_x и, в частности,

 

c_V = T (¶ S / ¶ T) _V. (37.2)

 

Поэтому

 

c_V = T (¶ S / ¶ T) _V = (¶ U / ¶ T) _V = (¶ U / ¶ S) _V / (¶² U / ¶ S ²) _V.

 

Или пусть интерес представляет изобарический коэффициент объемного расширения α _p = V ^–1(¶ V / ¶ T) _p:

 

α _p =

 

= V ^–1(¶ p / ¶ S) _V / ((¶ T / ¶ V) _S (¶ p / ¶ S) _V – (¶ T / ¶ S) _V (¶ p / ¶ V) _S) =

 

= V ^–1¶² U / (¶ S ¶ V) / ((¶² U / (¶ S ¶ V))² – (¶² U / ¶ S ²) _V (¶² U / ¶ V ²) _S)

и т. д. При адиабатическом процессе δ A = pdV = – dU, т. е. система совершает работу за счет внутренней энергии. Поэтому внутреннюю энергию называют также адиабатическим потенциалом.