Одно замечание о термодинамических функциях
Итак, каждый термодинамический потенциал, будучи известным в естественных переменных, содержит полную информацию о термодинамических свойствах системы. Если же термодинамическая функция задана не в естественных переменных, задача определения термодинамических свойств сводится к решению уравнения в частных производных и необходима дополнительная информация о системе. Пусть, к примеру, внутренняя энергия известна как функция температуры и объема. Потенциалом в этих переменных является свободная энергия. Для нахождения ее следует воспользоваться уравнением Гиббса–Гельмгольца (39.6). Его можно переписать следующим образом:
(¶(F / T) / ¶ T) V = – U / T 2.
Интегрирование по температуре дает свободную энергию с точностью до произвольной функции объема:
F (T, V) = – T Функцию φ(V) можно найти, если задать подходящее граничное условие. Подобная ситуация возникает и с другими термодинамическими потенциалами.
|
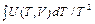+ T × φ(V).
