Преобразование Лежандра. Энтальпия
Другие термодинамические потенциалы можно получить с помощью преобразования Лежандра. В общем виде это выглядит следующим образом. Термодинамический потенциал L естественных переменных x, y, z, … имеет полный дифференциал dL = Xdx + Ydy + Zdz + …. Здесь X, Y, Z, … – функции переменных x, y, z, …. Преобразование Лежандра состоит в следующем. Вместо функции L и независимых переменных x, y, z, … вводятся новые переменные:
L ®
Тогда
d
Таким образом можно ввести энтальпию:
H = U + pV (38.3)
(здесь x = V, X = – p, L = U,
dH = TdS + Vdp. (38.4)
Условием того, что он полный, является соотношение Максвелла (еще одно)
(¶ T / ¶ p) S = (¶ V / ¶ S) p. (38.5)
Его легко получить, если перейти к якобиану и воспользоваться калибровочным соотношением (35.4):
(¶ T / ¶ p) S = ¶(T, S) / ¶(p, S) = ¶(p, V) / ¶(p, S) = (¶ V / ¶ S) p.
Коэффициенты в выражении (38.4) для dH определяются через частные производные от H:
T = (¶ H / ¶ S) p = T (S, p), V = (¶ H / ¶ p) S = V (S, p). (38.6)
Эту систему функций можно рассматривать как параметрическое задание термического уравнения состояния. Исключение параметра S приводит его к обычному виду. Внутренняя энергия находится из определения энтальпии (38.3):
U = H (S, p) – p × V (S, p) = U (S, p).
Исключение отсюда энтропии и давления (с помощью уравнений системы (38.6)) позволяет найти калорическое уравнение состояния. При желании можно получить другие термодинамические характеристики физической системы. Например:
cp = (δ Q / ¶ T) p = T (¶ S / ¶ T) p = T / (¶ T / ¶ S) p = (¶ H / ¶ S) p / (¶2 H / ¶ S 2) p.
При изобарических процессах (dH) p = T (dS) p = δ Qp = cpdT, откуда
cp = (¶ H / ¶ T) p. (38.7)
Физический смысл энтальпии при изобарических процессах объясняет ее другие названия: тепловая функция, теплосодержание.
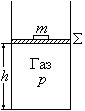
Убыль энтальпии при адиабатических процессах равна работе расширенной системы, состоящей, например, в случае газа в цилиндре под поршнем, из газа и поршня с грузом массы m (рис. 16). Полная энергия E такой системы равна внутренней энергии U газа и потенциальной энергии груза mgh = pV (p = mg / Σ, V = Σ h): E = U + pV = H. При адиабатических процессах расширенная система совершает работу за счет своей энергии:
δ Aрасш = – dE = – dH, или – dH = δ Aрасш.
39. Свободная энергия. Уравнение Гиббса–Гельмгольца
Однако использование функций U = U (S, V) и H = H (S, p) в качестве термодинамических потенциалов затруднено тем обстоятельством, что энтропия не может быть измерена непосредственно, подобно параметрам V, p и T. Если независимыми переменными являются температура и объем, то соответствующий термодинамический потенциал можно найти, преобразуя основное уравнение (29.9):
dU = TdS – pdV = d (TS) – SdT – pdV, или d (U – TS) = – SdT – pdV.
Функцию
F = U – TS (39.1)
называют свободной энергией (энергией Гельмгольца). Естественными переменными для нее являются температура и объем:
F = F (T, V). (39.2)
Полный дифференциал свободной энергии равен
dF = – SdT – pdV. (39.3)
При изотермических процессах система совершает работу за счет свободной энергии:
δ A = pdV = – (dF) T.
Величину TS называют связанной энергией. Соотношение взаимности можно получить, используя аппарат якобианов и соотношение (35.4):
– (¶ S / ¶ V) T = – ¶(T, S) / ¶(T, V) = – ¶(p, V) / ¶(T, V) = – (¶ p / ¶ T) V,
т. е.
(¶ S / ¶ V) T = (¶ p / ¶ T) V. (39.4)
Дифференцирование функции (39.2) по V и сравнение результата с коэффициентами равенства (39.3) позволяют получить термическое уравнение состояния:
p = – (¶ F / ¶ V) T = p (T, V). Аналогично находится энтропия
S = – (¶ F / ¶ T) V = S (T, V). (39.5)
Калорические свойства вещества можно установить, исключая энтропию (39.5) из формулы (39.1), определяющей свободную энергию:
U = F – T (¶ F / ¶ T) V. (39.6)
Это уравнение Гиббса–Гельмгольца. Свободную энергию также проблематично найти путем измерения. Сравнительно легко ее найти с точностью до слагаемого, зависящего только от температуры. Это можно сделать, вычислив изотермическую работу, совершаемую системой. Формула (39.6) позволяет с той же неопределенностью найти внутреннюю энергию системы. Вторые производные от функции F (T, V) позволяют определить калорические величины – теплоемкость cV и изотермический коэффициент сжимаемости γ:
cV = T (¶ S / ¶ T) V = – T (¶ F 2 / ¶ T 2) V,
γ = – V –1(¶ V / ¶ p) T (по определению) = –1/ (V (¶ p / ¶ V) T) = 1/ (V (¶ F 2 / ¶ V 2) T).
|

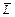 = L – Xx; x, y, z, … ® X, y, z, …. (38.1)
= L – Xx; x, y, z, … ® X, y, z, …. (38.1)