Примеры. 1. Материальная точка колеблется по закону x = sin wt

 

1. Материальная точка колеблется по закону x = sin w t. Найти вероятность того, что при случайном измерении ее положения она будет обнаружена в интервале x, x + dx.

Материальная точка совершает периодическое движение. Пусть полное время наблюдения за ней содержит чуть больше, чем n периодов. За один период (рис. 33, верхний график) она дважды окажется в интервале x, x + dx.

 

Рис. 33

 

Соответствующее время равно 2 dt. Тогда искомая вероятность равна

 

 

где T – период колебания, 0 £ q₁, q₂ < 1.

Из уравнения движения

 

dx = ω cos(ω t) · dt =

 

 

Откуда

 

dw (x) =

 

В результате плотность вероятности равна

 

 

Особенности при x = ±1 (рис. 33, нижний график) являются интегрируемыми. Можно проверить, что распределение нормировано:

 

 

т. е. площадь под кривой r(x) равна единице.

2. Найти среднее значение величины x, ее среднее квадратичное значение, среднюю квадратичную флуктуацию и относительную флуктуацию, если dw = const · exp(– a x) dx, 0 £ x £ ¥.

Очевидно, распределение имеет смысл только при a > 0 (иначе нормировать его не представляется возможным). Из условия нормировки

 

 

находится постоянная const =a. При этом вычисляется интеграл

 

.

 

В результате распределение принимает вид

dw =aexp (– a x) dx.

 

Для вычисления средних величин применяется дифференцирование по параметру

 

 

Квадратичная и относительная флуктуации находятся по формулам (78.2) и (78.3):

.

 

3. Идеальный газ содержит N молекул, заключенных в объеме V. Найти, какова вероятность того, что в выделенной мысленно части объема v содержится n молекул.

Вероятность обнаружить в объеме v одну выбранную молекулу равна v / V, две молекулы – (v / V)² и n выбранных молекул – (v / V) ⁿ. Аналогично, вероятность обнаружить выбранную молекулу в остальной части объема равна 1 – v / V, две молекулы – (1 – v / V)² и (N – n) молекул – (1 – v / V) ^{N – n}. В результате вероятность того, что в объеме v находится n выбранных молекул, а остальные (N – n) молекул находятся в другой части объема V, равна (v / V) ⁿ (1 – v / V) ^{N – n}. Число способов, которыми n произвольных молекул могут быть выбраны из общего числа молекул, равно числу сочетаний из N элементов по n: C_Nⁿ=N! / (n!(N – n)!). Полная вероятность нахождения в объеме v произвольно выбранных n молекул равна

w_N (n) = N! / (n!(N – n)!) (v / V) ⁿ (1 – v / V) ^{N – n}.

 

Это биноминальный закон. Из известной формулы (бином Ньютона)

 

 

следует, что полученное распределение нормировано на единицу.

Пользуясь биномом Ньютона и дифференцируя по параметру, можно найти среднее число частиц в объеме v. Действительно,

 

 

Тогда, если обозначить через a = v / V и b = 1 – v / V, то

 

 

Из биноминального закона могут быть получены формулы Пуассона при n << N и распределение Гаусса при n >> 1 и .
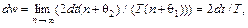
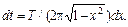
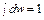
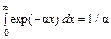
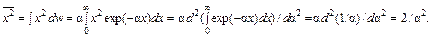