Давление идеального газа. Определение параметра a
В распределениях (82.15), (82.16) параметр a остался неопределенным. Его можно найти, если, пользуясь распределением (82.15), рассчитать давление газа p и сравнить его с давлением идеального газа
p = n RT / V. (83.1)
В процессе движения молекулы газа, заключенные в сосуд, испытывают соударения с его стенками. При этом каждая молекула передает отражающей ее стенке некоторый импульс. Давление газа на стенку сосуда равно суммарному импульсу, передаваемому единице площади стенки в единицу времени множеством ударяющихся о нее молекул. Если считать, что отражение молекул от стенки происходит совершенно упруго, то импульс, передаваемый при одном соударении, равен 2 mvx (ось x направлена перпендикулярно стенке). Пусть dj (vx) – число молекул, падающих на единицу площади стенки в единицу времени и имеющих x -ю компоненту скорости в интервале vx ¸ vx + dvx. Тогда давление газа равно
Для вычисления dj (vx) полезно обратиться к рис. 34, на котором схематически изображена область локализации молекул со скоростью Очевидно, dj (vx) равно числу молекул с данной компонетой скорости vx, находящихся в параллелепипеде высотой vx и основанием, равным единице площади: dj (vx) = vx dn (vx) = vx ndw (vx), (83.3)
где dn (vx) – концентрация молекул с данной компонентой скорости vx (в интервале vx ¸ vx + dvx), n – полная концентрация частиц (здесь концентрация – полное число частиц в единице объема). После подстановки выражения (83.3) в интеграл (83.2) для давления получается выражение
Рис. 34
Если воспользоваться теперь распределением (82.15), то
p = mn /(2a) = m n NА /(2a V), (83.6)
где NА – число Авогадро, n – число молей. Сравнение выражений (83.6) и (83.1) для p дает
a = m / (2 kT), (83.7) где k = R / NА = 1,38 × 10–16 эрг / K – постоянная Больцмана.
|

 (83.2)
(83.2) (параллелепипед), ударяющихся о стенку за единицу времени.
(параллелепипед), ударяющихся о стенку за единицу времени.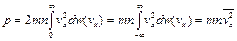 . (83.4)
. (83.4)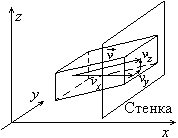
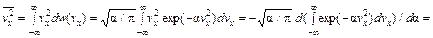
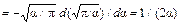 (83.5)
(83.5)


