Средние скорости и энергия молекул
С помощью распределения Максвелла можно найти средние значения разных величин. Для средней скорости молекул получается формула
Очевидно,
поэтому среднеквадратичная скорость с учетом результата (83.5) равна
Как средняя, так и среднеквадратичная скорость лишь не намного отличаются от наиболее вероятной:
Все эти скорости порядка скорости звука в газе. Для кислорода при комнатной температуре В соответствии с соотношением (85.3) средняя энергия поступательного движения молекулы равна
Эта энергия не зависит от массы молекулы. При комнатной температуре
Это частное проявление закона равнораспределения энергии по степеням свободы. Ранее он использовался в рамках термодинамики.
|

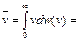

 . (85.1)
. (85.1)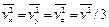 , (85.2)
, (85.2)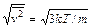 . (85.3)
. (85.3) (85.4)
(85.4)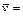 440 м / c, для водорода она в четыре раза больше.
440 м / c, для водорода она в четыре раза больше.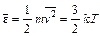 . (85.5)
. (85.5)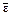 » 3/2 × 1,38 × 10 –16 × 293 × 10 –7 / (1,6 × 10 –19) = 0,04 эВ, что на два порядка меньше энергии связи атома в молекуле и недостаточно для диссоциации газа. На каждую степень свободы молекулы в среднем приходится одинаковая энергия
» 3/2 × 1,38 × 10 –16 × 293 × 10 –7 / (1,6 × 10 –19) = 0,04 эВ, что на два порядка меньше энергии связи атома в молекуле и недостаточно для диссоциации газа. На каждую степень свободы молекулы в среднем приходится одинаковая энергия . (85.6)
. (85.6)


