Распределение Максвелла. Вывод
Из предположения о хаотическом характере молекулярного движения следует, что возможно появление молекул с любой скоростью и искомое распределение будет характеризоваться непрерывной функцией. В связи с этим имеет смысл говорить не о числе молекул со строго заданной скоростью, а о числе молекул dn (
и о распределении вероятностей dw (
Поскольку распределение молекул по скоростям непрерывное, то можно ввести плотность вероятности g ( dw (
где d
g ( Аналогично можно ввести вероятность того, что молекула имеет компоненту скорости v x в дифференциально малом интервале v x¸ v x+ dv x:
dw (v x) = dn (v x) / n = f (v x) dv x, x = x, y, z, (82.5)
где, в силу хаотичности молекулярного движения, каждая из плотностей вероятностей зависит только от "своей" компоненты скорости и не зависит от других; больше того, вид этих функций распределения один и тот же независимо от выбора аргумента vx, vy или vz. Молекула имеет случайные значения трех компонент скорости. Обладание тем или иным значением одной компоненты скорости никак не зависит от величины других компонент. В соответствии с теоремой умножения вероятностей для независимых событий
dw (
Здесь под событием подразумевается обнаружение определенного значения одной из компонент скорости. Для плотностей вероятностей из (82.6) получается соотношение
Логарифмирование и последующее дифференцирование (82.7) по v x дает равенство
С учетом соотношения между компонентами и величиной скорости
уравнение (82.8) может быть представлено в виде
где a – константа, так как функции различных аргументов могут совпадать друг с другом во всей области их определения, если только они все равны одной и той же постоянной. Интегрирование уравнения (82.10) дает вид функций g (v) и f (v x):
Между постоянными интегрирования Z и Z 0, согласно соотношению (82.7), существует простая связь Z = Z 03. (82.12)
Постоянная Z 0 может быть найдена, если воспользоваться условием нормировки (82.2):
Разумеется, величина скорости и любая ее компонента ограничены скоростью света. Однако интегрирование в условии (82.13) можно распространить до бесконечности, если температура газа не слишком высока. При достижимых в земных условиях температурах доля быстрых молекул очень мала и вклад их в интеграл мал. Из условия нормировки (82.13) следует, что
Это так называемый интеграл Пуассона. Окончательно
Относительно параметра a можно сказать только, что он положительный. Это уже использовалось для удовлетворения условиям нормировки. Таким образом, предположение о статистической независимости движения в разных направлениях позволило найти распределение молекул по скоростям. Однако, сколько бы правдоподобной эта гипотеза ни казалась, она нуждается в экспериментальной проверке, в установлении границ ее применимости. Очевидно, что полученное распределение нельзя использовать при релятивистских скоростях. Если одна из компонент скорости равна скорости света, то две другие равны нулю: значение одной компоненты скорости зависит от величины двух других компонент. Идея о статистической независимости движения молекул по разным направлениям справедлива только для обычных нерелятивистских газов.
|

 ), имеющих скорость в некотором элементе объема пространства скоростей:
), имеющих скорость в некотором элементе объема пространства скоростей: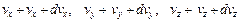 – (82.1)
– (82.1) . (82.2)
. (82.2) (82.7)
(82.7) . (82.8)
. (82.8) (82.9)
(82.9) (82.10)
(82.10)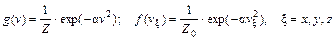 . (82.11)
. (82.11) . (82.13)
. (82.13) . (82.14)
. (82.14)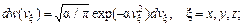 (82.15)
(82.15) . (82.16)
. (82.16)


