Свойства вероятности
Если вероятность некоторого события равна единице, то говорят, что событие достоверно, т. е. оно происходит в каждом испытании или измерении. Если, наоборот, вероятность равна нулю, то это невозможное событие. Если w (A) – вероятность события A, то вероятность того, что оно не произойдет, равна
Событие Суммой случайных событий A и B называют наступление события A либо B. Такое событие обозначают A + B. Если оба события взаимоисключающие, то из определения (75.1) вероятности следует, что w (A + B) = w (A) + w (B). (76.1)
Действительно, w (A + B) = Пусть для физической системы, которая может находиться в различных дискретных состояниях, известны вероятности wi и wj ее нахождения в состояниях i и j. Это взаимоисключающие события. Время пребывания системы в одном из состояний i и j – безразлично, в каком именно – равно сумме времен пребывания в каждом из них. Поэтому вероятность того, что система находится в одном из этих состояний, равна
Вероятность нахождения системы в одном из двух взаимоисключающих состояний равна сумме вероятностей нахождения системы в каждом из состояний. Формулы (76.1) и (76.2) выражают закон (теорему) сложения вероятностей. Теорема сложения вероятностей может быть без всякого труда перенесена на случай трех или большего числа состояний. В общем случае вероятность того, что система находится в одном из взаимоисключающих состояний i, j, k, …, равна
Из теоремы сложения вероятностей вытекает важное следствие. Пусть состояние системы характеризуется двумя не зависящими друг от друга величинами L и M. Величина L может пробегать дискретный ряд значений L 1, L 2, …, а M – значения M 1, M 2, … Пусть известна вероятность
где суммирование ведется по всем значениям величины M. Важным следствием закона сложения вероятностей является весьма очевидное утверждение, что вероятность нахождения системы в произвольном допустимом состоянии равна единице. Попросту говоря, в каком-либо из состояний система с достоверностью находится. Справедливость утверждения видна из того, что
так как, по определению, Если величины, характеризующие состояние системы, изменяются непрерывно, то последнее равенство преобразуется к виду
В дальнейшем все вероятности считаются нормированными на единицу, и если это не так, проводится соответствующее нормирование. Произведением событий A и B называется событие, в котором происходят и A, и B одновременно. Его обозначают AB. Если события независимы, то имеет место закон (теорема) умножения вероятностей
w (AB) = w (A) w (B). (76.7)
Если для двух совершенно независимых физических систем обозначить через
Закон умножения вероятностей представляет строгое определение статистической независимости двух систем. Это положение можно пояснить следующим расчетом. Пусть первая из двух произвольных независимых физических систем проводит время Закон умножения вероятностей можно еще пояснить на простом примере, когда кроме одной молекулы совершенно произвольно выбирается вторая и вычисляется вероятность того, что обе молекулы одновременно окажутся в объеме v, являющемся частью объема V. Эта вероятность равна (v / V)2.
|

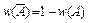 .
.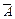 называют дополнительным к A.
называют дополнительным к A.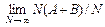 =
= 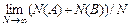 – получается формула (76.1).
– получается формула (76.1).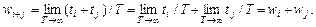 (76.2)
(76.2)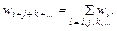 (76.3)
(76.3)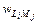 того, что система находится в состоянии, в котором L = Li и M = Mj. Спрашивается, какова вероятность
того, что система находится в состоянии, в котором L = Li и M = Mj. Спрашивается, какова вероятность  того, что система имеет значение Li при любом значении величины M. Согласно теореме сложения вероятностей, можно написать
того, что система имеет значение Li при любом значении величины M. Согласно теореме сложения вероятностей, можно написать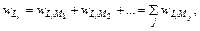 (76.4)
(76.4) , (76.5)
, (76.5)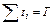 .
.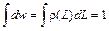 . (76.6)
. (76.6)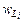 и
и  вероятности того, что первая система находится в состоянии, характеризуемом величиной Li, и, аналогично, вторая – в состоянии, характеризуемом Mj, то, согласно теореме (76.7), вероятность одновременной реализации состояний с L = Li и M = Mj равна произведению вероятностей
вероятности того, что первая система находится в состоянии, характеризуемом величиной Li, и, аналогично, вторая – в состоянии, характеризуемом Mj, то, согласно теореме (76.7), вероятность одновременной реализации состояний с L = Li и M = Mj равна произведению вероятностей  (76.8)
(76.8)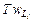 в состоянии с L = Li (T – общее время наблюдения). Если время
в состоянии с L = Li (T – общее время наблюдения). Если время  в состоянии с M = Mj. Вероятность одновременного нахождения первой системы в состоянии с L = Li и второй в состоянии с M = Mj равна
в состоянии с M = Mj. Вероятность одновременного нахождения первой системы в состоянии с L = Li и второй в состоянии с M = Mj равна 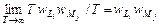 .
.


