Флуктуации
Возникает естественный вопрос, в какой мере задание среднего значения характеризует реальное значение величины. Ясно, что если отклонения величины от своего среднего значения достаточно малы, то всегда можно без большой погрешности заменить истинное значение величины ее средним значением. Для точного же количественного ответа необходимо ввести некоторую величину, которая характеризовала бы отклонение истинных значений L от ее среднего
который называется квадратичной флуктуацией (дисперсией распределения wL). Квадратичная флуктуация существенно положительная величина. Всякое отклонение от среднего вносит свой вклад в ее значение (отклонения от
Помимо квадратичной вводится относительная флуктуация
Последняя дает возможность оценить относительную погрешность, которая возникает при замене L ее средним значением В рамках теории вероятности доказывается следующая теорема: если имеется система, состоящая из N независимых частей, то относительная флуктуация любой аддитивной функции состояния L системы обратно пропорциональна квадратному корню из числа N, т. е.
Задачей теоретической физики является изучение свойств макроскопических систем, состоящих из огромного числа атомов или молекул. Применение статистических законов позволяет находить средние значения разных величин, характеризующих состояние системы. Из приведенной теоремы следует, что относительные флуктуации всех физических величин, значение которых для всей системы равно сумме значений их для всех частиц, обратно пропорционально квадратному корню из числа частиц. Поскольку число частиц в макроскопических системах выражается огромными числами (в одном моле число частиц NA = 6 × 1023), относительная флуктуация любой аддитивной величины (например, энергии, энтропии) оказывается практически равной нулю (для моля d l ~ 10 –12). Это означает, что все аддитивные величины имеют значения, весьма близкие к средним. Поэтому замена истинных величин их средними значениями может быть произведена с очень большой точностью. Таким образом, вероятностные предсказания приобретают практически достоверный характер.
|

 . В качестве такого критерия вводится средний квадрат разности
. В качестве такого критерия вводится средний квадрат разности (78.1)
(78.1) мала, то значение величины L все время близко к своему среднему значению
мала, то значение величины L все время близко к своему среднему значению  . (78.2)
. (78.2)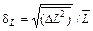 . (78.3)
. (78.3) . (78.4)
. (78.4)


